9 Глава 1.
Введение в математическую статистику
1.1. Измерения и измерительные шкалы в психологических исследованиях
В ходе психологического эксперимента мы получаем числовые данные, которые являются результатами измерительных процедур разного рода. Давайте разберемся, что же понимается под измерением в психологических исследованиях? В обиходе, когда мы говорим «измерить» длину, площадь, объем, вес, температуру или другие физические величины, то представляем себе привычную процедуру: возьмем мерку и при помощи измерительного инструмента — линейки, палетки, мерного стакана, весов, термометра и др. — посмотрим, сколько раз она укладывается в измеряемом предмете. Однако в психологии и педагогике все не так просто. Эти науки изучают такие сложные явления и процессы, что придумать для них «мерку» практически невозможно. Кроме того, если до предмета можно дотронуться, увидеть его, ощутить его вес или температуру, то как «пощупать» воображение, «увидеть» память или «ощутить» мышление другого человека?
И все же измерения в психологии тоже широко применяются. Уточним, что понимается при этом под измерением. Измерение — это приписывание чисел некоторым свойствам испытуемых по определенным правилам. Правила могут быть самыми разными. Например, при определении уровня развития зрительной памяти детей по методике А. Н. Леонтьева ребенку предъявляется последовательность из 10 символов — математических знаков — и предлагается их запомнить. Количество правильно воспроизведенных символов фиксируется, тем самым каждому ребенку приписывается
10число от 0 до 10, отражающее его развитие зрительной памяти. Другое правило используется для определения уровня развития смысловой памяти по методике В. И. Яшиной. Ребенку читают текст и просят его пересказать. Исследователь оценивает пересказ ребенка по шести параметрам, таким как понимание текста, структурирование текста, лексика, грамматика, плавность речи, самостоятельность пересказа, и за каждый из них ставится от 0, 1 или 2 балла. Итоговая оценка — сумма баллов по всем параметрам — может варьироваться, таким образом, от 0 до 12 баллов. При определении мотивационной готовности ребенка к школе реакции ребенка на группу типовых вопросов ставят в соответствие число 1, 2 или 3, отражающее низкий, средний или высокий ее уровень. Значение измерений заключается в том, что они позволяют сравнивать измеряемое свойство у разных испытуемых: понятно, что смысловая память лучше развита у ребенка, получившего 10 баллов, чем у ребенка, получившего только 5 баллов. Измерения предоставляют нам объективный эмпирический материал, который дает возможность сделать психологическое исследование более обоснованным. Кроме того, они помогают установить нормы развития различных психических процессов.
Каждому выбранному правилу соответствует свой тип измерений. В настоящее время во всем мире применяется следующая классификация измерительных шкал, предложенная в 1950-е годы американским ученым С. Стивенсом: 1) шкалы наименований (другие названия — номинативные, номинальные); 2) шкалы порядка (или же ранговые, ординальные); 3) шкалы интервалов; 4) шкалы отношений. В каждой последующей шкале используются не только свойства чисел предыдущей шкалы, но и дополнительные свойства, поэтому шкалы более высокого порядка, то есть имеющие больший порядковый номер, позволяют выполнять больше операций над числами и предоставляют больше возможностей для математической
11обработки. Номинативные и порядковые шкалы называются качественными, интервальные и шкалы отношений — количественными. Охарактеризуем теперь шкалы каждого типа более подробно.
Измерение по шкале наименований — это просто классификация. Да-да, как это ни удивительно, но как только мы использовали классификацию испытуемых по некоторому свойству, тем самым мы уже измерили это свойство. Испытуемых группируют в классы, классам приписывают названия. Роль названий могут играть числа. Эти числа характеризуют только равенство или различие испытуемых в отношении измеряемого свойства. Сравнение чисел и арифметические операции с ними бессмысленны.
Например, если мы определили пол у детей старшей группы детского сада, то есть разбили группу на мальчиков и девочек, тем самым мы произвели номинативное измерение. Можно оставить эти названия, но можно и заменить их числами, скажем, девочкам мы сопоставим число 1, а мальчикам число 2. Это не количество девочек или мальчиков, а просто некоторые символы, заменяющие слова «девочка» или «мальчик». Числа здесь играют роль меток, и сравнивать их не имеет смысла: нельзя быть девочкой в большей или меньшей степени. Легко понять, что вместо выбранных чисел можно взять любые другие, ведь ничего кроме равенства или различия детей в отношении пола они не означают. Другой пример — национальность. Предположим, в нашей группе есть узбеки (1), русские (2) и якуты (3). Всем известно, что 1+2=3, но что может означать фраза «узбек плюс русский равняется якуту»? Клинические диагнозы, типы темпераментов, преобладающие типы психологической защиты, акцентуации характера, стили руководства, типы детских игр — все это примеры номинативных измерений, весьма распространенных в психологии.
12Более тонкая шкала — шкала порядка. Порядковое измерение возможно, если экспериментатор может определить различные степени проявления измеряемого свойства. Испытуемым приписывают числа либо в прямом порядке (то есть чем сильнее выражено свойство, тем больше число), либо в обратном (чем слабее выражено свойство, тем больше число). Полученные числа можно сравнивать, но нельзя выполнять с ними арифметические операции. Равные разности чисел не отражают равных разностей в количествах измеряемого свойства. Нет единицы измерения.
Поясним сказанное на примерах. Классический пример — конкурс красоты. Предположим, что перед нами стоят четыре девушки — Аня, Маша, Даша, Катя, — и мы просим какого-либо молодого человека проранжировать их по красоте, то есть назвать самую красивую, менее красивую и так далее. Любой молодой человек с легкостью сделает это. Пусть красивее всех он посчитал Катю, и мы присвоили ей число 100, далее оказались Аня (50), Маша (49) и, наконец, Даша (1). На первый взгляд, Дашу можно пожалеть, но все совсем не так плохо — ведь шкала порядковая. Действительно, 100–50=50, но нельзя сказать, что Катя красивее Ани на 50 каких-то единиц, ведь таких единиц не существует. Действительно, индивидуальные пристрастия в отношении женской красоты настолько расходятся, что нет ни единственно красивой женщины, ни единицы измерения красоты. Возможно даже, что другой молодой человек в соответствии со своими предпочтениями именно Дашу назовет самой красивой.
Другой классический пример — школьные оценки. Нельзя сказать, на сколько больше знаний у ученика, получившего на экзамене 5, чем у ученика, получившего 3. Примеры измерений по шкале порядка из области психологии: степень согласия с утверждением; уровень развития речи; степень мотивационной
13готовности к школе; самооценка степени развития коммуникативных навыков; степень обобщенности сенсорных эталонов. Примеры можно было бы множить, так как данный тип шкал наиболее распространен в этой области.
Порядковые шкалы могут быть более грубыми (3—5 градаций типа «низкий, средний, высокий уровень»; «ниже нормы», «норма», «выше нормы» или «абсолютно согласен, скорее согласен, не знаю, скорее не согласен, абсолютно не согласен») или более дифференцированными (от 6—8 ступенек). Последние, разумеется, предпочтительнее, так как позволяют более тонко оценить свойство.
Измерение по интервальной шкале позволяет определить, на сколько единиц сильнее проявляется свойство у одного испытуемого, чем у другого. Здесь есть единица измерения. Числа можно складывать, вычитать, умножать и делить на коэффициент. Ноль не фиксирован и не указывает на отсутствие свойства. Отношение приписанных чисел бессмысленно.
Классическим примером интервальной шкалы является температурная шкала Цельсия. Действительно, нулевой отметке соответствует температура таяния льда, отметке в 100 градусов — температура кипения воды. Этот температурный промежуток разделен на 100 интервалов, и один такой интервал и есть один градус. Он является единицей измерения. Если вчера было 5 градусов тепла, а сегодня — 10 градусов, то мы говорим, что сегодня на 5 градусов теплее, чем вчера. Однако мы не можем сказать, что сегодня вдвое теплее, чем вчера, так как ноль в шкале Цельсия — условная точка отсчета, и она может быть смещена. Другой классический пример — летосчисление. В григорианском календаре начало отсчета — рождество Христово, в других календарях оно может быть другим. Новый год может также отмечаться не только в ночь с 31 декабря на 1 января, но и весной или осенью. Единственное, что объединяет все
14календари — длительность года, который продолжается 365 дней. Именно за этот период Земля совершает один оборот вокруг Солнца, и это — объективно существующая единица измерения.
По вопросу о наличии интервальных шкал в психологии мнения специалистов расходятся. Строго говоря, в психологии практически нет интервальных шкал. Действительно, единица измерения должна быть той же природы, что и измеряемое свойство, но что такое единица внимания, тревожности или креативности? Вместе с тем, с некоторой натяжкой, показатели, измеренные по хорошо дифференцированным шкалам, представляющим собой стандартизованные тесты, таким как тест Стенфорда – Бине или тест Векслера для определения коэффициента интеллекта, принято обрабатывать как интервальные.
Особенность шкал отношений по сравнению со шкалами интервалов — наличие абсолютного нуля, который означает отсутствие измеряемого свойства. В них с полученными числами можно выполнять все арифметические операции, а отношения чисел отражают количественные отношения измеряемого свойства. Классический пример такой шкалы — температура по Кельвину. Как известно, температура тела определяется скоростью движения молекул: чем быстрее они движутся, тем температура выше. Нулевой отметкой в шкале Кельвина считается такая, при которой движение молекул прекращается — это абсолютный ноль. В психологии и педагогике такие шкалы встречаются, если измеряются физические величины — рост, вес, время решения задачи, скорость реакции на стимул, количество допущенных ошибок и др. Шкалы отношений встречаются также в психофизике при измерении абсолютных порогов чувствительности в физических единицах свойств стимула.
К сказанному добавим следующее. Как уже упоминалось выше, балльные оценки, представляют собой порядковую шкалу измерений,
15так как балл, вообще говоря, не является единицей измерения. В теории измерений существуют известные методы перевода «сырых» тестовых баллов в стандартные шкалы, такие как Z-шкала, T-шкала, шкала стенов. Тем самым порядковые измерения переводятся в метрические, где за единицу измерения берутся доли стандартного отклонения или она устанавливается в соответствии с процентильными границами групп в нормальном распределении стандартной шкалы. Обсуждение данного вопроса выходит за рамки настоящего пособия.
Однако в психологическом сообществе дифференцированные порядковые измерения часто трактуются как интервальные. По-видимому, это связано с тем, что с определенной натяжкой балл все же можно соотнести с небольшой долей измеряемого свойства, и чем более дифференцирована шкала, тем более мы склонны доверять такой трактовке. В случае грубых порядковых шкал, например, трехбалльных шкал типа «ниже нормы – норма – выше нормы», балл уже не считается единицей измерения и представляет собой, скорее, метку или обозначение категории, то есть такие шкалы по своим свойствам близки к номинативным. Отметим, что многие представленные в этой книге методы статистического анализа данных пригодны уже для номинативных либо порядковых шкал (это каждый раз оговаривается).
Существует также общепринятая практика математической обработки, обусловленная правилами и ограничениями применения статистических критериев. Согласно ей, номинативные и грубые порядковые измерения (условно, до 3—5 градаций) принято обрабатывать одними методами, а более дифференцированные (скажем, от 6—8 градаций) — другими. К сожалению, четкого разграничения здесь провести нельзя. Кроме того, измерения по шкалам интервалов и шкалам отношений — количественные
16измерения — обрабатываются одними и теми же методами, поэтому в статистическом пакете SPSS при обозначении шкалы измерений есть всего три категории — номинальные, порядковые и количественные шкалы. Добавим, что в новых версиях SPSS, начиная с 18-й, номинативные измерения так и обозначаются «номинальными», грубые порядковые обозначаются «порядковыми», а все измерения, начиная с дифференцированных порядковых, обозначаются как «количественные». Программа не допускает выполнения даже таких операций, как критерий Манна – Уитни или критерий Краскела – Уоллиса, с переменными, обозначенными не как «количественные».
1.2. Важнейшие типы распределений случайных величин
Характеристики, измеряемые в эмпирических исследованиях по психологии и педагогике с помощью тестов и других диагностических методик, называются переменными, признаками или случайными величинами. Такими характеристиками могут быть интеллект, тревожность, креативность, различные виды памяти, учебная мотивация и т. д. Случайными величинами они являются потому, что в процессе психологической диагностики их значения невозможно предугадать заранее. Можно лишь указать вероятности того, что случайная величина принимает то или иное значение или попадает в некоторый интервал. Случайные величины возникают в психологии также в процессе проверки статистических гипотез, о которых пойдет речь ниже. Случайная величина описывается законом распределения вероятностей, который помогает исследователю сделать вывод о принятии или отклонении статистической гипотезы, вычислить доверительный интервал, определить возрастные нормы развития психических функций и т. д. Рассмотрим самые важные законы распределения, ниболее часто используемые на практике.
17Нормальное распределение. Непрерывная случайная величина X имеет нормальное распределение с параметрами μ и σ, если она задается плотностью распределения 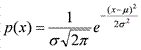 . Вероятностный смысл параметров μ и σ: μ=MX — математическое ожидание случайной величины X; σ2=DX — ее дисперсия и σ — стандартное отклонение. Форма записи: X ~ N(μ, σ). Нормальная кривая изображена на рис. 1. Площадь под любой такой кривой равна 1.
. Вероятностный смысл параметров μ и σ: μ=MX — математическое ожидание случайной величины X; σ2=DX — ее дисперсия и σ — стандартное отклонение. Форма записи: X ~ N(μ, σ). Нормальная кривая изображена на рис. 1. Площадь под любой такой кривой равна 1.
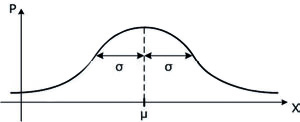
Рис. 1. Нормальная кривая
Случайная величина X имеет стандартное нормальное распределение, если μ=0 и σ=1. В этом случае формула ее плотности приобретает вид 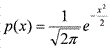 , а записывается этот факт так: X ~ N(0, 1). Кривая, заданная этой формулой, называется стандартной нормальной кривой (рис. 2).
, а записывается этот факт так: X ~ N(0, 1). Кривая, заданная этой формулой, называется стандартной нормальной кривой (рис. 2).
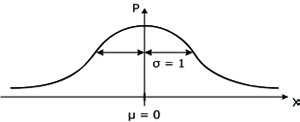
Рис. 2. Стандартная нормальная кривая
Если случайная величина X имеет нормальное распределение с параметрами μ и σ, то нормированная случайная величина 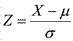 имеет стандартное нормальное распределение, т. е. Z ~ N(0, 1). Для вычисления вероятностей используется функция Лапласа Φ(x),
имеет стандартное нормальное распределение, т. е. Z ~ N(0, 1). Для вычисления вероятностей используется функция Лапласа Φ(x),
18заданная формулой: 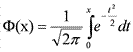 . Ее значения для разных x можно найти в таблице (см. табл. 4 Приложения). Поскольку Φ(x) — нечетная функция, т. е. Φ(–x)=–Φ(x), то ее таблицы составлены только для x≥0. Геометрический смысл этой функции: ее значение для некоторого x>0 равно площади под стандартной нормальной кривой над отрезком от 0 до x (рис. 3).
. Ее значения для разных x можно найти в таблице (см. табл. 4 Приложения). Поскольку Φ(x) — нечетная функция, т. е. Φ(–x)=–Φ(x), то ее таблицы составлены только для x≥0. Геометрический смысл этой функции: ее значение для некоторого x>0 равно площади под стандартной нормальной кривой над отрезком от 0 до x (рис. 3).
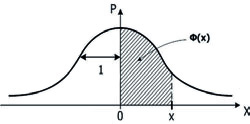
Рис. 3. Геометрический смысл функции Лапласа
Для стандартной нормальной случайной величины ее функция распределения F(x)=0,5+Φ(x), а вероятность того, что она примет значение в интервале [a, b], выражается формулой
P(a≤X≤b)=F(b)–F(a)=Φ(b)–Φ(a). Если же случайная величина X распределена нормально с произвольными параметрами μ и σ, то ее функция распределения выражается формулой 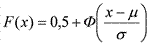 , а вероятность попадания ее значений в интервал [a, b] — формулой
, а вероятность попадания ее значений в интервал [a, b] — формулой 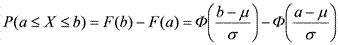 . Отсюда легко следует, что для симметричного относительно μ интервала [μ–kσ, μ+kσ] вероятность попадания в него значений нашей нормальной случайной величины X ~ N(μ, σ) выражается следующей формулой:
. Отсюда легко следует, что для симметричного относительно μ интервала [μ–kσ, μ+kσ] вероятность попадания в него значений нашей нормальной случайной величины X ~ N(μ, σ) выражается следующей формулой:
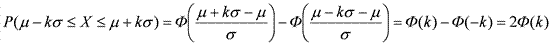 .
.
Особенно важны для психологии два частных случая этой формулы для k=1 и k=3. При k=1 справедливо P(μ–σ, μ+σ)=2Φ(1)=2⋅0,3413=0,6826≈0,68, т. е. для нормально
19распределенной случайной величины с параметрами μ и σ вероятность того, что она примет значение в интервале [μ–σ, μ+σ], приближенно равна 0,68. Аналогично для k=3 имеем
P(μ–3σ, μ+3σ)=2Φ(3)=2⋅0,49865=0,9973. Это так называемое «правило трех сигм»: для нормально распределенной случайной величины с параметрами μ и σ вероятность попасть в интервал [μ–3σ, μ+3σ] превышает 0,99 (рис. 4).
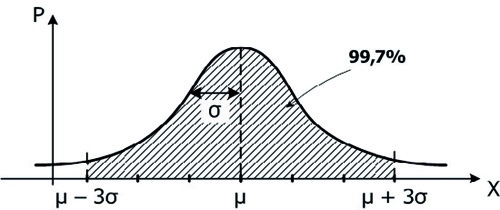
Рис. 4. Иллюстрация «правила трех сигм»
Нормальное распределение признака играет в психологии особую роль. Во-первых, при стандартизации тестов очень благоприятна ситуация, когда стандартизационная выборка нормальна: это косвенно свидетельствует о ее репрезентативности и дает возможность определить нормы для этого теста. Так, например, для нормального распределения нормой обычно считается интервал значений тестовых баллов в пределах [μ–σ, μ+σ]. Кроме того, перевод «сырых» баллов в z-значения или T-значения также основан на нормальном распределении. Во-вторых, при количественном анализе эмпирических данных нередко используются статистические критерии, необходимым условием применения которых является условие нормальности — это t-критерий Стьюдента, F-критерий Фишера, коэффициент корреляции Пирсона, ANOVA и т. д. Такие методы называются параметрическими.
Распределения, связанные с нормальным. При операциях с нормальными случайными величинами часто возникает 3 новых вида рспределений: распределение Хи-квадрат, t-распределение Стьюдента
20и F-распределение Фишера. В математической статистике они используются, например, при вычислении доверительных интервалов для нормальных параметров. Распределение статистик многих критериев, использующихся для проверки различных предположений, хорошо приближается этими распределениями.
Пусть случайные величины X1, X2, ..., Xn — независимы, и каждая из них имеет стандартное нормальное распределение N(0, 1). Говорят, что случайная величина 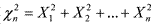 имеет распределение Хи-квадрат с n степенями свободы. Для любого n≥1 эта случайная величина с вероятностью 1 принимает положительные значения. На рис. 5 изображены функции плотности распределения Хи-квадрат для n=3 (сплошная линия) и n=8 (пунктир). Площадь под любой такой кривой равна единице.
имеет распределение Хи-квадрат с n степенями свободы. Для любого n≥1 эта случайная величина с вероятностью 1 принимает положительные значения. На рис. 5 изображены функции плотности распределения Хи-квадрат для n=3 (сплошная линия) и n=8 (пунктир). Площадь под любой такой кривой равна единице.
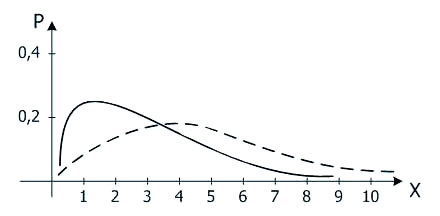
Рис. 5. Функции плотности распределения Хи-квадрат с числом степеней свободы n=3 и n=8
В табл. 1 Приложения приведены значения 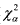 , соответствующие вероятности
, соответствующие вероятности 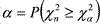 распределения с Хи-квадрат с n=df степенями свободы. Это такие точки
распределения с Хи-квадрат с n=df степенями свободы. Это такие точки 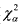 на оси значений случайной величины Хи-квадрат, правее которых лежит площадь под кривой плотности распределения
на оси значений случайной величины Хи-квадрат, правее которых лежит площадь под кривой плотности распределения 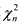 , равная α.
, равная α.
Пусть снова имеются независимые случайные величины X0, X1, X2, ..., Xn, имеющие стандартное нормальное распределение N(0, 1). Тогда случайная величина 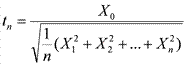 имеет t – распределение
имеет t – распределение
21Стьюдента с n степенями свободы. Кривая ее плотности симметрична относительно оси x=0. При больших n эта кривая приближается к стандартной нормальной кривой. На рис. 6 изображены функции плотности распределения Стьюдента для n=1 (пунктир) и n=100 (сплошная линия).
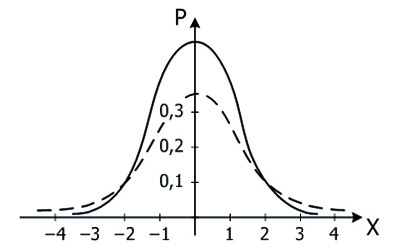
Рис. 6. Функции плотности распределения Стьюдента с числом степеней свободы n=1 и n=10
В таблице 8 Приложения приведены значения tα для различных вероятностей α=P(|tn|≥tα) t – распределения Стьюдента с n=df степенями свободы. Они представляют собой такие точки на оси значений случайной величины t, что левее точки (–tα) и правее точки tα лежит по α/2 площади под кривой плотности распределения Стьюдента, в сумме дающие α. При этом площадь под всей кривой равна 1.
Наконец, F-распределение Фишера задается следующим образом. Пусть имеются независимые случайные величины Y1, Y2, ..., Ym и X1, X2, ..., Xn, все имеющие стандартное нормальное распределение N(0, 1). Тогда случайная величина 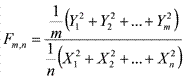 имеет распределение Фишера с числом степеней свободы m и n. Легко видеть, что F-распределение связано с t-распределением простым соотношением:
имеет распределение Фишера с числом степеней свободы m и n. Легко видеть, что F-распределение связано с t-распределением простым соотношением: 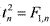 . На рис. 7 изображены функции плотности распределения Фишера с числами
. На рис. 7 изображены функции плотности распределения Фишера с числами
22степеней свободы m=1, n=4 (сплошная линия) и m=10, n=50 (пунктир).
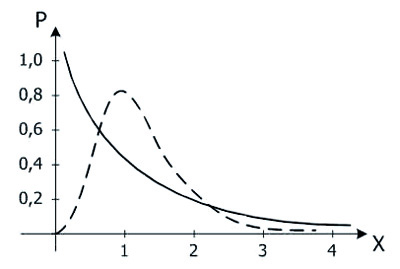
Рис. 7. Функции плотности распределения Фишера с числом степеней свободы m=1, n=4 и m=10, n=50
Поскольку семейство F-распределений зависит от двух параметров m и n, то таблицы довольно громоздски. В Приложении приведена таблица 7 для α=0,05 и 0,01. В них указаны значения Fα, такие что P(Fm,n≥Fα)=α, для чисел степеней свободы m=df1 и n=df2 F-распределения. Если выбрать конкретную кривую F-распределения, то Fα — это точка на оси абсцисс, правее которой лежит площадь под этой кривой, равная α. Площадь под всей кривой равна 1.
Равномерное распределение. Случайная величина X имеет равномерное распределение на отрезке [a, b], если она задается плотностью вероятностей ![latex:p(x)=\{{\begin array {l} c=\frac{1}{b-a}при x\in[{a,b}]\\ 0\;при x\notin[{a,b}]\\\end array}](pictures/MMa-022PG.gif) . Эта запись означает, что если x принадлежит отрезку [a, b], то
. Эта запись означает, что если x принадлежит отрезку [a, b], то 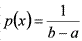 , а вне этого отрезка p(x)=0 (рис. 8).
, а вне этого отрезка p(x)=0 (рис. 8).
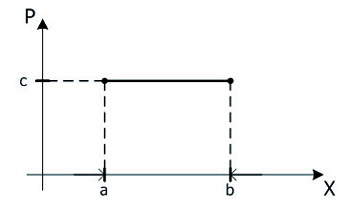
Рис. 8. График плотности равномерного распределения
23Добавим, что вероятность P(α≤X≤β) попадания значений равномерно распределенной случайной величины в интервал [α, β], лежащий внутри отрезка [a, b], равна 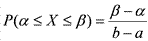 . Она зависит только от длины интервала [α, β], но не зависит от его положения на отрезке [a, b].
. Она зависит только от длины интервала [α, β], но не зависит от его положения на отрезке [a, b].
1.3. Методы описательной статистики
Пусть требуется изучить некоторое свойство у очень большой группы людей. На практике сплошное обследование всей группы не проводят, так как это невозможно по организационным, финансовым и другим причинам. Действительно, чтобы обследовать всех детей, обучающихся по программе «Радуга», нужно посетить все детские сады, реализующие эту программу, а масштабы нашей страны не позволяют этого сделать. Вместо этого из всей совокупности людей случайным образом отбирают ограниченное число людей и работают с ними. Эта совокупность случайно отобранных людей называется выборочной совокупностью или выборкой, а совокупность людей, из которых производится выборка, называется генеральной совокупностью. Часто под генеральной совокупностью понимают множество всех мысленно возможных людей интересующего нас типа, например, детей 5-го года жизни, для которых в заданных условиях изучается один или несколько признаков или свойств. В психологических исследованиях такими признаками являются психологические и педагогические характеристики: уровень тревожности, продуктивность вербальной памяти, мотивационная готовность к школе, уровень знаний по предмету и т. д.
Для того чтобы по выборке можно было уверенно судить о генеральной совокупности, выборка должна быть репрезентативной, т. е. достаточно хорошо, без искажений представлять генеральную совокупность. Репрезентативность выборки обеспечивается
24случайностью отбора. Например, если мы изучаем интеллект и учебную мотивацию в генеральной совокупности школьников Москвы, то для получения репрезентативной выборки можно отобрать по несколько школ из каждого округа, общей численностью до 40 школ, и протестировать всех учащихся, например, 6-х — 10-х классов, присутствующих на занятиях. Если же для стандартизации некоторого теста нам нужна репрезентативная выборка относительно более широкой генеральной совокупности, нужно позаботиться, чтобы в нее вошли представители обоих полов, разного уровня образования, разных социальных слоев и т. д.
Объемом выборочной или генеральной совокупности называется число объектов в этой совокупности. Например, если из 2000 человек случайным образом выбраны 50, то объем генеральной совокупности N=2000 и объем выборки n=50. Поскольку объем генеральной совокупности, как правило, значительно превышает объем выборки, то принимают, что генеральная совокупность имеет бесконечный объем. Такое допущение оправдывается еще и тем, что знание объема генеральной совокупности не используется при обработке выборочных данных. Выборки каких же объемов лучше использовать в реальных исследованиях? Жестких рекомендаций на этот счет нет, однако, чем меньше выборки, тем более грубыми будут результаты их обработки и тем труднее с их помощью выявить достоверные различия. Минимальный объем выборок определяется, как правило, статистическими таблицами критических значений для того или иного критерия проверки статистических гипотез: в таблице просто не указываются критические значения для очень малых выборок. Чаще всего берутся выборки объемов от 20 до 30 испытуемых, однако они могут быть и меньше.
Вместе с тем, сразу предостережем читателя: ориентироваться на малые выборки не нужно, поскольку такой объем статистического
25материала, разумеется, не может быть удовлетворительным для серьезного научного исследования. Ни один солидный научный журнал не возьмет статью для публикации, если результаты получены на малых выборках, и это совершенно справедливо. Согласно практике, принятой в психологическом научном сообществе, объемы выборок должны быть не менее 30 испытуемых, а если сравнивается 4—5 групп или более, то общий объем получается порядка 150—200 человек. В серьезных исследованиях объемы выборок доходят до нескольких тысяч. Именно к таким объемам и надо стремиться.
Методы описания выборок с помощью различных показателей и графиков называются методами описательной статистики. Они помогают компактно описать совокупность наблюдений с помощью информативных статистических показателей, таких как полигон и гистограмма распределения, различные выборочные характеристики. Перейдем к их рассмотрению.
Полигон и гистограмма распределения
Пусть у нас имеется некоторая выборка, и мы хотели бы представить эту информацию графически. Если измерения количественные, простейшим способом графического представления данных является полигон распределения. Рассмотрим пример.
Пример 1.3.1
У группы испытуемых (n=14) определялась продуктивность вербальной памяти. Тестовый балл — количество фамилий писателей и поэтов, которых испытуемый вспомнил за 5 минут. Данные: 23, 23, 20, 27, 28, 23, 25, 25, 23, 20, 29, 23, 25, 27. Построить полигон распределения.
Решение примера 1.3.1
1) Построить вариационный ряд, упорядочив элементы выборки по возрастанию: 20, 20, 23, 23, 23, 23, 23, 25, 25, 25, 27, 27, 28, 29. Член вариационного ряда называется вариантой.
262) Построить распределение частот, заполнив таблицу:
xi | ni |
20 | 2 |
23 | 5 |
25 | 3 |
27 | 2 |
28 | 1 |
29 | 1 |
3) Изобразить это распределение графически (рис. 9):
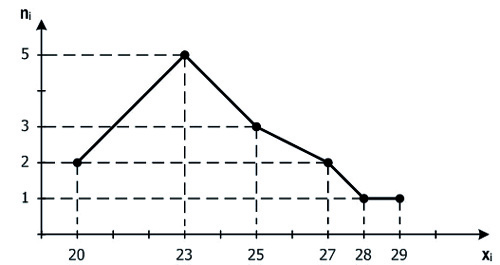
Рис. 9. Полигон распределения показателей продуктивности вербальной памяти
При больших выборках удобнее обобщенное представление данных в виде распределения сгруппированных частот. Графическое изображение распределения частот попадания элементов выборки в соответствующие интервалы группировки называется частотной гистограммой выборки (далее будем называть ее просто гистограммой). Иными словами, гистограмма это совокупность столбцов, каждый из которых опирается на один разрядный интервал, а их высоты отражают частоты попадания тестовых баллов в каждый из разрядных интервалов. Покажем на примере алгоритм построения гистограммы.
Пример 1.3.2
Рассмотрим показатели интеллекта по тесту Стенфорда – Бине
27у группы из 75 испытуемых (n=75). Построить гистограмму распределения этих показателей.
141 | 127 | 118 | 102 | 97 | 121 | 113 | 123 |
92 | 95 | 124 | 92 | 101 | 130 | 114 | 107 |
100 | 109 | 111 | 94 | 116 | 91 | 106 | 107 |
132 | 108 | 135 | 101 | 112 | 92 | 105 | 129 |
97 | 104 | 110 | 115 | 113 | 101 | 102 | 106 |
110 | 104 | 110 | 124 | 95 | 146 | 139 | |
106 | 87 | 127 | 98 | 108 | 105 | 86 | |
107 | 133 | 114 | 118 | 123 | 121 | 107 | |
105 | 89 | 105 | 105 | 102 | 108 | 148 | |
83 | 134 | 103 | 138 | 131 | 129 | 96 | |
Решение примера 1.3.2
Для построения гистограммы нужно сделать 4 шага.
1) Определить размах выборки, равный разности между максимальным и минимальным тестовым баллом в выборке. В нашем случае размах равен xmax–xmin=148—83=65 баллам.
2) Выбрать длину интервала группировки. Рекомендуется так выбирать интервал группировки, чтобы у нас получилось 10—15 интервалов, следовательно, столбцов гистограммы. Удобно также выбирать целочисленный интервал или интервал, оканчивающийся на пять десятых. Если мы возьмем 15 интервалов, то длина каждого из них будет равна 65:15=4,3; при 14 интервалах длина каждого составит 65:14=4,6; при 13 интервалах длина одного интервала будет 65:14=5. На этом мы можем остановиться и положить длину интервала группировки равной 5. Заметим, что если бы у нас снова получилось неподходящее число, мы бы продолжили методом проб и ошибок делить размах на 12, 11, 10 равных частей. Разумеется, не всегда получается выбрать удобную длину интервала группировки,
28тогда можно взять любую и полученных ранее длин и строить гистограмму с использованием приближенной длины интервала.
3) Заполнить таблицу следующего вида:
Номер
интервала | Границы
интервала | Подсчет | Частота |
1 | [83, 88] | | | | | 3 |
2 | (88, 93] | | | | | | | 5 |
3 | (93, 98] | | | | | | | | | 7 |
4 | (98, 103] | | | | | | | | | | 8 |
5 | (103, 108] | | | | | | | | | | | | | | | | | | | 17 |
6 | (108, 113] | | | | | | | | | | 8 |
7 | (113, 118] | | | | | | | | 6 |
8 | (118, 123] | | | | | | 4 |
9 | (123, 128] | | | | | | 4 |
10 | (128, 133] | | | | | | | | 6 |
11 | (133, 138] | | | | | 3 |
12 | (138, 143] | | | | 2 |
13 | (143, 148] | | | | 2 |
В первом столбце таблицы находятся порядковые номера интервалов группировки с 1 по 13-й. Второй столбец содержит координаты левого и правого конца интервалов. Далее мы будем считать, сколько тестовых баллов попадает в каждый конкретный интервал группировки. Куда же причислять балл, попавший на границу двух соседних интервалов группировки? Договоримся, что каждый граничный балл будем относить к предыдущему, то есть к левому интервалу, поэтому правый конец каждого интервала обозначим квадратной скобкой, а левый конец — круглой скобкой. Это означает, что левый конец не принадлежит интервалу, а правый — принадлежит.
Чтобы заполнить третий столбец, рассмотрим первый по счету балл в нашей выборке: 141. Этот балл попадает в 13-й интервал, поэтому в таблице рядом с этим интервалом поставим вертикальную
29палочку, а балл 141 вычеркнем из массива: мы его уже использовали. Следующий балл 92 относится ко 2-му интервалу, и мы ставим в таблице вертикальную палочку рядом с этим интервалом, а балл 92 вычеркиваем из массива и т. д. Если балл попал на границу интервалов, например 123, то палочку ставим рядом с 8-м интервалом. Когда процесс завершится, остается только посчитать палочки рядом с каждым интервалом и записать частоту в последнем столбике.
4) Теперь можно нарисовать гистограмму, выбрав систему координат и отложив по оси абсцисс границы интервалов группировки, а по оси ординат — частоты (рис. 10).
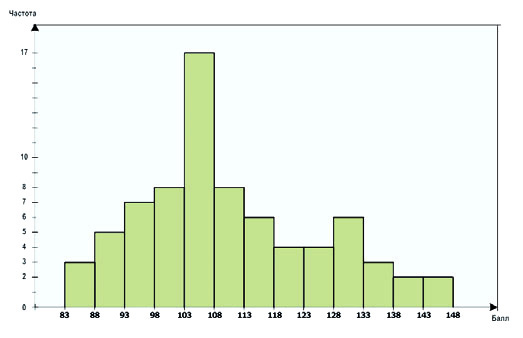
Рис. 10. Гистограмма распределения показателей интеллекта
Построение гистограммы в статистическом пакете SPSS
Процедура ввода и обозначения данных в SPSS с 18 версии практически не отличается от аналогичной процедуры для предыдущих версий. Особое внимание следует уделить обозначению шкалы измерений, так как программа контролирует соответствие типа шкалы выбранному методу обработки. Важно отметить, что номинативная шкала здесь обозначается как Nominal/Номинальная, грубая порядковая шкала как Ordinal/Порядковая, а любая шкала, начиная с дифференцированной порядковой, обозначается как
30Scale/Количественная. Основное отличие новых версий программы при построении гистограмм и других диаграмм состоит в заказе самой процедуры построения.
Ввод и обозначение данных. Тестовые баллы нажатием клавиши «Enter» на клавиатуре вводим в один столбец — в одну переменную, например, в первую var00001.
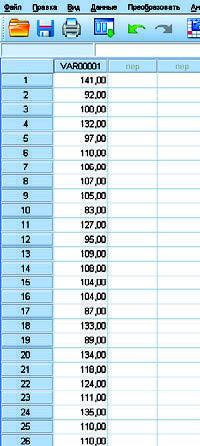
Рис. 11. Ввод и обозначение данных в SPSS
Для обозначения переменной нажать клавишу Variable View/Переменные в левом нижнем углу экрана. В строчке, соответствующей переменной var00001, в ячейке Name/Имя ввести имя нашей переменной, например, IQ/КИ, т. е. коэффициент интеллекта. В ячейке Label/Метка можно записать то же наименование, но можно также использовать более подробное наименование из нескольких слов, например, «intellectual quotient/КИ». Кроме того, нужно определить шкалу измерений в клетке Measure/Шкала: Scale/Количественная. Нажатием клавиши Data View/Данные вернуться к столбцу данных.
31Процедура построения гистограммы. В верхней строке нажать Graphs/Графика, затем Chart Builder/Конструктор диаграмм.
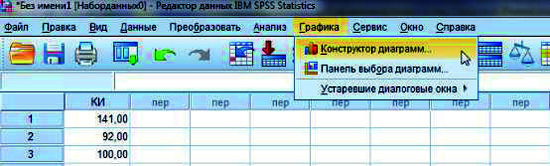
Рис. 12. Процедура построения гистограммы в SPSS
В появившемся окне, состоящем из нескольких окон, нажать кнопку Gallery/Галерея. В рамке под заголовком Choose from/Выберите из выбрать Histogram/Гистограмма. В окне правее появится несколько картинок — разных вариантов гистограмм. Выбрать самую первую картинку Simple Histogram/Простая гистограмма.
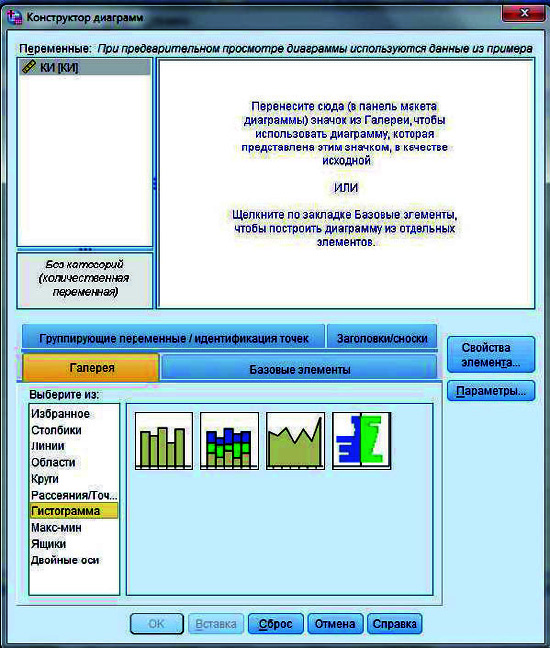
Рис. 13. Процедура построения гистограммы в SPSS
32Переместить выбранную картинку в широкое окно в правом верхнем углу, над которым написано Chart preview uses example data/При предварительном просмотре диаграммы используются данные из примера. Открывается окно Element Properties/Свойства элемента. Переместить нашу переменную «intellectual quotient/КИ» из окошка Variables/Переменные на X-Axis/Ось X под схематическим рисунком гистограммы, тогда на Y-Axis/Ось Y появится слово Histogram/Гистограмма.
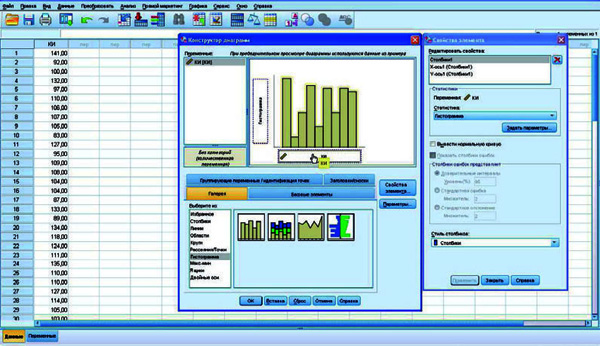
Рис. 14. Процедура построения гистограммы в SPSS
Можно также при желании в окне Element Properties/Свойства элемента выделить X-Axis1 (Bar1)/X-ось1 (Столбики 1) и заменить Axis Label/Метка оси на другое наименование. Можно также, но не обязательно, заказать Display normal curve/Вывести нормальную кривую и нажать кнопку Apply/Применить. Еще можно нажать на кнопку Titles/Footnotes — Заголовки/Сноски и обозначить более подробно, распределение каких показателей представлено на гистограмме. По окончании этих процедур нажать ОК. В результате на экране появится гистограмма.
33Гистограмма распределения показателей по тесту интеллекта по Стенфорду-Бине
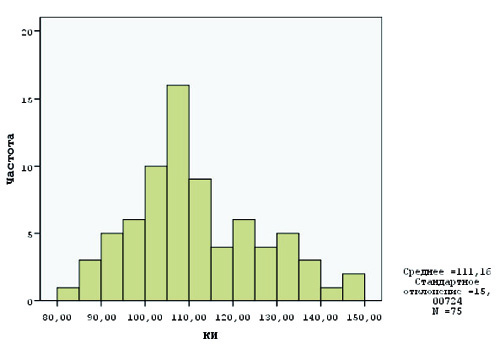
Рис. 15. Гистограмма в SPSS
Выборочные характеристики
Для описания выборки помимо графиков используются информативные статистические показатели, которые способны избавить исследователя от просмотра сотен, а порой и тысяч значений выборки. Среди выборочных характеристик выделяются меры центральной тенденции, меры изменчивости и меры положения. Меры центральной тенденции отражают уровень выраженности измеренного признака. К ним относятся среднее, медиана, мода. Меры изменчивости применяются для численного выражения величины вариативности признака и включают выборочные дисперсию, стандартное отклонение, асимметрию, эксцесс. Меры положения — это различные квантили, т. е. точки на оси баллов, которые делят всю совокупность выборочных данных на несколько равных по численности групп: процентили (процентные точки) P1, P2, ..., P99 — на 100 групп, квартили Q1, Q2, Q3 — на 4 группы, децили — на 10 групп. Медиане соответствует процентиль Р50, квартилям — процентили P25, P50, P75, а децилям — процентили P10, P20, ..., P90.
Сначала рассмотрим 3 наиболее употребительные характеристики выборки: среднее, дисперсию и стандартное отклонение.
34 Пример 1.3.3
Даны результаты тестирования группы из n=28 испытуемых. Определялась продуктивность вербальной памяти. Тестовым баллом было количество фамилий писателей и поэтов всех времен и народов, которые испытуемые могли вспомнить за 5 минут.
39 | 30 | 28 | 29 | 31 | 39 | 32 |
24 | 27 | 26 | 35 | 37 | 31 | 29 |
32 | 30 | 36 | 50 | 31 | 30 | 29 |
40 | 23 | 37 | 20 | 40 | 37 | 24 |
Вычислить выборочные среднее, дисперсию, стандартное отклонение.
Решение примера 1.3.3
Прежде чем вычислять выборочные характеристики, построим вариационный ряд и распределение частот. Вариационный ряд это последовательность тестовых баллов, расположенных в порядке возрастания. Чтобы построить вариационный ряд, найдем в нашей выборке минимальный показатель, запишем его отдельно и вычеркнем его из выборки, из оставшихся показателей снова выберем наименьший, запишем его справа от первого и т. д. Получим следующий вариационный ряд: 20, 23, 24, 24, 26, 27, 28, 29, 29, 29, 30, 30, 30, 31, 31, 31, 32, 32, 35, 36, 37, 37, 37, 39, 39, 40, 40, 50.
Распределение частот это соотношение между показателями выборки и частотами их встречаемости в выборке. Его легко построить, используя вариационный ряд.
Выборочное среднее показывает, сколько тестовых баллов в среднем получили испытуемые, и вычисляется по формуле: 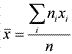 , где хi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. Для его вычисления удобно использовать расчетную таблицу, в первых двух столбцах которой располагается
, где хi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. Для его вычисления удобно использовать расчетную таблицу, в первых двух столбцах которой располагается
35распределение частот, а в третьем — всевозможные произведения вариант на соответствующие частоты:
xi | ni | ni⋅xi |
20 | 1 | 20 |
23 | 1 | 23 |
24 | 2 | 48 |
26 | 1 | 26 |
27 | 1 | 27 |
28 | 1 | 28 |
29 | 3 | 87 |
30 | 3 | 90 |
31 | 3 | 93 |
32 | 2 | 64 |
35 | 1 | 35 |
36 | 1 | 36 |
37 | 3 | 111 |
39 | 2 | 78 |
40 | 2 | 80 |
50 | 1 | 50 |
Сумма | 896 |
Складывая числа в третьем столбце, найдем сумму 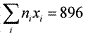 . Разделим ее на объем выборки n=28 и получим выборочное среднее 32. Таким образом, в среднем наши испытуемые получили по 32 балла.
. Разделим ее на объем выборки n=28 и получим выборочное среднее 32. Таким образом, в среднем наши испытуемые получили по 32 балла.
Выборочная дисперсия характеризует разброс показателей вокруг своего выборочного среднего: чем больше разброс, тем больше дисперсия. Она вычисляется по формуле: 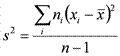 , где —
, где — 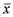 — выборочное среднее, xi — i-я по порядку варианта, ni — частота i-й
— выборочное среднее, xi — i-я по порядку варианта, ni — частота i-й
36варианты, n — объем выборки. Для ее вычисления используем расчетную таблицу:
xi | ni | 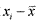
| 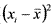
| 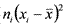
|
20 | 1 | –12 | 144 | 144 |
23 | 1 | –9 | 81 | 81 |
24 | 2 | –8 | 64 | 128 |
26 | 1 | –6 | 36 | 36 |
27 | 1 | –5 | 25 | 25 |
28 | 1 | –4 | 16 | 16 |
29 | 3 | –3 | 9 | 27 |
30 | 3 | –2 | 4 | 12 |
31 | 3 | –1 | 1 | 3 |
32 | 2 | 0 | 0 | 0 |
35 | 1 | 3 | 9 | 9 |
36 | 1 | 4 | 16 | 16 |
37 | 3 | 5 | 25 | 75 |
39 | 2 | 7 | 49 | 98 |
40 | 2 | 8 | 64 | 128 |
50 | 1 | 18 | 324 | 324 |
Сумма | 1122 |
Первые два столбца таблицы содержат распределение частот. Числа в третьем столбце получаются вычитанием выборочного среднего из чисел первого столбца. В четвертом столбце числа из третьего столбца возводятся в квадрат, а в последнем пятом столбце числа четвертого столбца умножаются на частоты второго столбца. Суммируя числа в пятом столбце, получим 1122. Разделив эту сумму на (n—1), получим искомую выборочную дисперсию s2=41,6. Чтобы найти выборочное стандартное отклонение по формуле 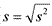 , извлечем квадратный корень из выборочной дисперсии, получим s=6,4.
, извлечем квадратный корень из выборочной дисперсии, получим s=6,4.
37Обратимся теперь к другим выборочным характеристикам. Медиана — это такое число, которое делит вариационный ряд на 2 равные части. Если объем выборки n=2k+1, то xmed=x(k+1), а если n=2k, то 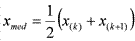 . Например, если вариационный ряд состоит из n=5 показателей 20, 23, 24, 24, 26, то xmed=x(3)=24, а если из n=14 показателей 20, 20, 23, 23, 23, 23, 23, 25, 25, 25, 27, 27, 28, 29, то
. Например, если вариационный ряд состоит из n=5 показателей 20, 23, 24, 24, 26, то xmed=x(3)=24, а если из n=14 показателей 20, 20, 23, 23, 23, 23, 23, 25, 25, 25, 27, 27, 28, 29, то 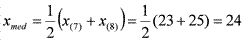 . Медиана — это 50-й процентиль P50. Мода xmod — это наиболее часто встречающееся значение в выборке. Бывают распределения, в которых 2 моды — бимодальные — или несколько мод — полимодальные. Например, в выборке 20, 20, 23, 23, 23, 23, 23, 25, 25, 25, 27, 27, 28, 29 модой является значение 23.
. Медиана — это 50-й процентиль P50. Мода xmod — это наиболее часто встречающееся значение в выборке. Бывают распределения, в которых 2 моды — бимодальные — или несколько мод — полимодальные. Например, в выборке 20, 20, 23, 23, 23, 23, 23, 25, 25, 25, 27, 27, 28, 29 модой является значение 23.
Асимметрия характеризует «скошенность» распределения, то есть преобладание в гистограмме малых или, наоборот, больших значений признака и вычисляется по формуле: 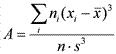 , где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу, но при больших выборках значения, вычисленные по обеим этим формулам практически совпадают. Приведем пример, где для упрощения расчетов возьмем из примера 1.3.3 первые 5 показателей: 20, 23, 24, 24, 26 (для этой выборки n=5,
, где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу, но при больших выборках значения, вычисленные по обеим этим формулам практически совпадают. Приведем пример, где для упрощения расчетов возьмем из примера 1.3.3 первые 5 показателей: 20, 23, 24, 24, 26 (для этой выборки n=5, 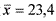 , s=2,2). Расчетная таблица:
, s=2,2). Расчетная таблица:
xi | ni | 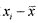
| 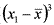
| 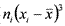
|
20 | 1 | –3,4 | –39,3 | –39,3 |
23 | 1 | –0,4 | –0,1 | –0,1 |
24 | 2 | 0,6 | 0,2 | 0,4 |
26 | 1 | 2,6 | 17,6 | 17,6 |
Сумма | –21,4 |
38Отсюда 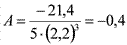 . Знак показателя асимметрии указывает, в какую сторону отклоняется кривая распределения от симметричного вида относительно среднего значения. Если A>0, то асимметрия левосторонняя, т. е. в распределении преобладают низкие показатели. При A<0 имеем правостороннюю асимметрию с преобладанием высоких показателей. Симметричная кривая, например, нормальная, имеет A=0 (рис. 16).
. Знак показателя асимметрии указывает, в какую сторону отклоняется кривая распределения от симметричного вида относительно среднего значения. Если A>0, то асимметрия левосторонняя, т. е. в распределении преобладают низкие показатели. При A<0 имеем правостороннюю асимметрию с преобладанием высоких показателей. Симметричная кривая, например, нормальная, имеет A=0 (рис. 16).
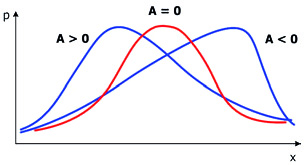
Рис. 16. Форма кривой распределения при разной асимметрии
Эксцесс — мера остроконечности или плосковершинности гистограммы распределения. Он вычисляется по формуле 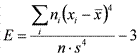 . При E>0 показатели тесно группируются около среднего значения, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Кривая нормального распределения имеет E=0 (рис. 17).
. При E>0 показатели тесно группируются около среднего значения, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Кривая нормального распределения имеет E=0 (рис. 17).
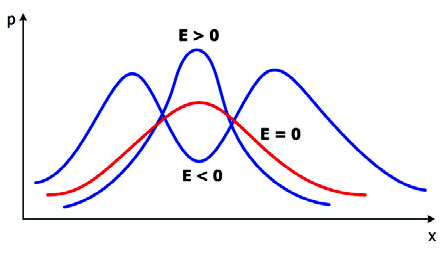
Рис. 17. Форма кривой распределения при разном эксцессе
39Вычислим эксцесс для нашего примера 1.3.3, снова взяв те же первые 5 показателей, что и при вычислении асимметрии.
xi | ni | 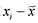
| 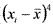
| 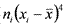
|
20 | 1 | –3,4 | 133,6 | 133,6 |
23 | 1 | –0,4 | 0 | 0 |
24 | 2 | 0,6 | 0,1 | 0,2 |
26 | 1 | 2,6 | 45,7 | 45,7 |
Сумма | 179,5 |
Отсюда 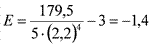 .
.
Вычисление выборочных характеристик в статистическом пакете SPSS
Ввод и обозначение данных. Тестовые баллы вводим в одну переменную, набирая число на клавиатуре и нажимая клавишу «Enter». Для обозначения переменной нажимаем клавишу Variable View/Переменные в левом нижнем углу экрана. Обозначим имя переменной, введя в клетку Name/Имя слово «pamjat/память». В клетке Label/Метка запишем наименование переменной более распространенно, например «verbalnaja pamjat/вербальная память». Обозначим шкалу измерений Measure/Шкала: Scale/Количественная.
Процедура вычисления выборочных характеристик. Нажмем Analyse/Анализ, затем Descriptive Statistics/Описательные статистики, Frequencies/Частоты. Выделим интересующую нас переменную и перебросим ее в широкое окошко Variable(s)/Переменные. Уже заказана операция Display frequency tables/Вывести частотные таблицы (если нам это не нужно — просто отменим ее). Нажмем кнопку Statistics/Статистики, в окошке Central Tendency/Расположение отметим галочкой Mean/Среднее; в окошке Dispersion/Разброс отметим Std. Deviation/Стандартное отклонение и
40Variance/Дисперсия. Кроме того, закажем Quartiles/Квартили, Skewness/Асимметрия и Kurtosis/Эксцесс. Нажмем Continue/Продолжить и OK.
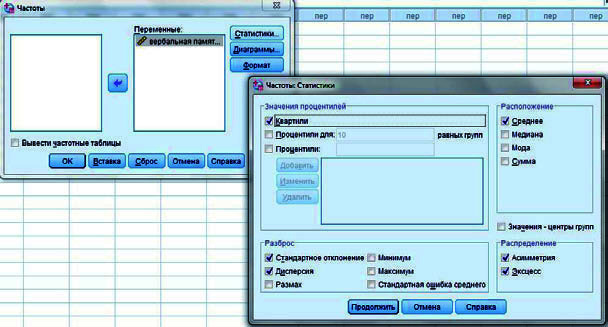
Рис. 18. Процедура вычисления выборочных характеристик в SPSS
Для введенных данных из примера 1.3.3 о продуктивности вербальной памяти получим таблицу, в которой указаны искомые выборочные характеристики:
Статистики
вербальная память | | |
N | Валидные | 28 |
Пропущенные | 0 |
Среднее | | 32,0000 |
Стд. отклонение | | 6,44636 |
Дисперсия | | 41,556 |
Асимметрия | | ,598 |
Стд. ошибка асимметрии | | ,441 |
Эксцесс | | ,872 |
Стд. ошибка эксцесса | | ,858 |
Процентили | 25 | 28,2500 |
50 | 31,0000 |
75 | 37,0000 |
Рис. 19. Таблица с выборочными характеристиками в SPSS
41 Задачи для самостоятельного решения
Задача 1.3.4
Даны результаты группы из n=100 испытуемых по тесту интеллекта Стенфорда – Бине. Построить гистограмму распределения показателей интеллекта.
106 | 107 | 107 | 95 | 143 | 103 | 140 | 125 | 120 | 123 |
125 | 93 | 99 | 145 | 130 | 120 | 121 | 116 | 127 | 117 |
92 | 125 | 135 | 124 | 100 | 120 | 110 | 140 | 138 | 117 |
130 | 130 | 141 | 118 | 134 | 118 | 87 | 119 | 124 | 117 |
124 | 98 | 92 | 146 | 125 | 108 | 138 | 133 | 111 | 105 |
136 | 100 | 93 | 112 | 128 | 109 | 125 | 111 | 128 | 113 |
143 | 100 | 111 | 87 | 90 | 94 | 109 | 145 | 109 | 118 |
93 | 86 | 113 | 130 | 121 | 132 | 134 | 115 | 116 | 121 |
117 | 131 | 123 | 113 | 121 | 140 | 94 | 125 | 115 | 95 |
117 | 140 | 99 | 113 | 144 | 140 | 103 | 100 | 110 | 94 |
Задача 1.3.5
Рассмотрим подвыборки, состоящие из первых 10-ти показателей выборки из задачи 1.3.4, затем из последующих 10-ти ее показателей и т. д. Вычислить для каждой из них выборочные харатеристики: среднее, дисперсию, стандартное отклонение, асимметрию, эксцесс.
Точечные и интервальные оценки характеристик генеральной совокупности
Все выборочные характеристики — это точечные оценки соответствующих характеристик генеральной совокупности. В статистике под термином «оценка» понимается приближенное значение некоторой величины. Точечными они называются потому, что определяются одним числом. Так, точечными оценками генерального среднего, дисперсии, стандартного отклонения, асимметрии, эксцесса являются выборочные среднее, дисперсия,





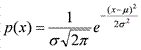 . Вероятностный смысл параметров
. Вероятностный смысл параметров 

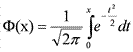 . Ее значения для разных x можно найти в таблице (см. табл. 4 Приложения). Поскольку
. Ее значения для разных x можно найти в таблице (см. табл. 4 Приложения). Поскольку 


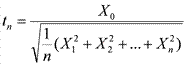 имеет t – распределение
имеет t – распределение
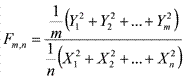 имеет распределение Фишера с числом степеней свободы m и n. Легко видеть, что F-распределение связано с t-распределением простым соотношением:
имеет распределение Фишера с числом степеней свободы m и n. Легко видеть, что F-распределение связано с t-распределением простым соотношением: 
![latex:p(x)=\{{\begin array {l} c=\frac{1}{b-a}при x\in[{a,b}]\\ 0\;при x\notin[{a,b}]\\\end array}](pictures/MMa-022PG.gif) . Эта запись означает, что если x принадлежит отрезку [a, b], то
. Эта запись означает, что если x принадлежит отрезку [a, b], то 







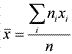 , где
, где 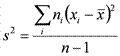 , где —
, где — 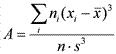 , где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу, но при больших выборках значения, вычисленные по обеим этим формулам практически совпадают. Приведем пример, где для упрощения расчетов возьмем из примера 1.3.3 первые 5 показателей: 20, 23, 24, 24, 26 (для этой выборки n=5,
, где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу, но при больших выборках значения, вычисленные по обеим этим формулам практически совпадают. Приведем пример, где для упрощения расчетов возьмем из примера 1.3.3 первые 5 показателей: 20, 23, 24, 24, 26 (для этой выборки n=5, 
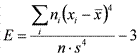 . При E>0 показатели тесно группируются около среднего значения, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Кривая нормального распределения имеет E=0 (рис. 17).
. При E>0 показатели тесно группируются около среднего значения, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Кривая нормального распределения имеет E=0 (рис. 17).


