1 M. G. Sorokova
MAHEMATICAL METHODS
IN PSYCHO-EDUCATIONAL
RESEARCHES
TEXTBOOK
Recommended by the Academic Council
of the Moscow State University
of Psychology and Education for students studying
in the fields of training
37.03.01 Psychology, 37.04.01 Psychology,
44.04.02 Psychological and Pedagogical Education,
specialties
37.05.01 Clinical Psychology,
44.05.01 Pedagogy and psychology
of deviant behavior
Moscow, 2020
2М. Г. Сорокова
МАТЕМАТИЧЕСКИЕ МЕТОДЫ
В ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ
ИССЛЕДОВАНИЯХ
УЧЕБНОЕ ПОСОБИЕ
Рекомендовано Ученым советом Московского государственного психолого-
педагогического университета для студентов, обучающихся
по направлениям подготовки
37.03.01 Психология, 37.04.01 Психология,
44.04.02 Психолого-педагогическое образование,
специальностей
37.05.01 Клиническая психология,
44.05.01 Педагогика
и психология девиантного
поведения
Москва 2020
3
Рецензенты:
| | Л. С. Куравский — доктор технических наук, профессор, заведующий кафедрой «Прикладная информатика и мультимедийные технологии», декан факультета «Информационные технологии» Московского государственного психолого-педагогического университета К. К. Абгарян — доктор физико-математических наук, доцент, заведующая отделом Федерального исследовательского центра «Информатика и управление» Российской академии наук |
| | Сорокова М. Г. |
С65 | Математические методы в психолого-педагогических исследованиях: Учебное пособие. — М.: Неолит, 2020. — 216 с. ISBN 978-5-6043562-0-3 В учебном пособии в простой и доступной форме изложены методы математической статистики, широко применяемые для анализа данных эмпирических исследований в психологии и педагогике. Приведены примеры решения кейс-заданий в статистическом пакете SPSS. Материал представлен на русском и английском языках и может использоваться также при обучении иностранных студентов прикладной математической статистике и в курсах английского языка для психологов и педагогов. Адресовано студентам бакалавриата, магистратуры, аспирантам, широкому кругу исследователей в области психологии и педагогики. |
ISBN 978-5-6043562-0-3 | © Сорокова М. Г., 2020 © Издательский дом «Неолит», 2020 |
5 Оглавление
| | | | |
Введение | 6 |
Глава 1. Введение в математическую статистику | 8 |
| | 1.1 Измерения и измерительные шкалы в психолого-педагогических исследованиях | 8 |
| | 1.2 Генеральная совокупность и выборка, графическое представление данных | 12 |
| | 1.3 Статистические оценки параметров распределения | 19 |
| | 1.4 Проверка статистических гипотез: общие положения | 24 |
Глава 2. Одновыборочные и двухвыборочные задачи | 28 |
| | 2.1 Выявление различий между двумя независимыми выборками: критерий Манна — Уитни | 28 |
| | 2.2 Выявление различий между двумя связными выборками: критерий знаковых ранговых сумм Уилкоксона | 35 |
| | 2.3 Выявление различий между двумя распределениями: критерий однородности Хи-квадрат для двух независимых выборок | 42 |
| | 2.4 Проверка равномерности распределения: критерий согласия Хи-квадрат | 51 |
| | 2.5 Проверка нормальности распределения: критерий Колмогорова — Смирнова | 57 |
| | 2.6 Проверка равенства дисперсий и средних двух нормальных генеральных совокупностей. Критерии Фишера и Стьюдента | 62 |
Глава 3. Однофакторный анализ. Анализ связи признаков | 67 |
| | 3.1 Однофакторный анализ: критерии Краскела — Уоллиса, Джонкхиера, однофакторный дисперсионный анализ ANOVA | 67 |
| | | Критерий Краскела — Уоллиса в SPSS | 70 |
| | | Критерий Джонкхиера в SPSS | 73 |
| | | ANOVA в SPSS | 76 |
| | 3.2 Однофакторный анализ с повторными измерениями: критерий Фридмана | 82 |
| | | Критерий Фридмана в SPSS | 84 |
| | 3.3 Коэффициент корреляции Пирсона и простая линейная регрессия. Коэффициент ранговой корреляции Спирмена | 88 |
| | | Коэффициент корреляции Пирсона в SPSS | 91 |
| | | Коэффициент ранговой корреляции Спирмена в SPSS | 94 |
| | 3.4 Выявление связи признаков: критерий независимости Хи-квадрат | 97 |
Заключение | 108 |
Рекомендуемая литература | 109 |
6 Введение
Уважаемые коллеги, наш курс называется «Математические методы в психолого-педагогических исследованиях», так как и в психологии, и в педагогике используются одинаковые количественные методы. Выбор метода определяется не областью знаний, а характером поставленной задачи и типом измерений. Цель курса — сформировать компетенции, необходимые для количественного анализа эмпирических данных психолого-педагогических исследований в статистическом пакете SPSS. Задачи курса — ознакомить обучающихся с основными понятиями и методами математической статистики, используемыми в современных психологии и образовании, и сформировать практические навыки количественного анализа эмпирических данных в SPSS у студентов бакалавриата, магистратуры, аспирантуры и широкого круга исследователей. SPSS или Statistical Package for Social Sciences — это современная компьютерная программа международного класса, в которой есть весь арсенал методов, необходимых исследователю в области психологии и образования. Почему же этот курс так важен и каковы его достоинства?
Во-первых, он актуален. Современное эмпирическое исследование в психологии и педагогике, выполненное в естественно-научной методологии, невозможно без математики. Действительно, если одна или несколько групп обследованы с помощью методик разного типа, то образуется большая база данных — числовая матрица. Это большая таблица чисел, из которой нужно извлечь информацию и сделать содержательный вывод. Проверить гипотезу исследования можно только с использованием адекватных методов количественного анализа данных.
Математическая статистика активно применяется в психологии и педагогике как за рубежом, так и в России. Для публикации статьи в серьезных научных журналах, индексируемых в Web of Science или Scopus, выводы должны быть доказательными. Для этого необходимо представить результаты количественного анализа эмпирических данных.
Во-вторых, курс «Математические методы в психолого-педагогических исследованиях» носит выраженный практический характер. Изложение материала максимально приближено к тематике психолого-педагогических исследований, а основное внимание уделено решению типовых задач. Решая задачи, начинающие исследователи не только приобретают опыт количественного анализа, но и получают возможность действовать по образцу.
В-третьих, мы старались изложить материал в доступной форме и максимально простым языком. Разумеется, доступность изложения не означает, что нужно отказаться от математической терминологии: студенты должны ею владеть. Хорошо известно, однако, что в основе любой математической теории,
7лежат простые идеи. Эти идеи мы и пытались донести до студентов. Особое внимание уделено интерпретации результатов. При таком подходе курс значительно выигрывает в ясности и привлекательности для студентов.
В-четвертых, мы хорошо понимаем: чтобы сформировать у студентов исследовательские компетенции, нужно научить их анализировать эмпирические данные на компьютере в SPSS. Статистический пакет SPSS создан специально для социальных наук, признан и широко применяется во всем мире. Компьютерная обработка не только экономит время и исключает вычислительные ошибки, но и стимулирует к увеличению объемов выборок. Действительно, программа SPSS обрабатывает данные выборок из нескольких тысяч испытуемых с той же легкостью, что и всего ста.
Заметим, что мы не будем заниматься расчетами по сложным формулам, а будем делать три шага или отвечать на три вопроса: 1. Какие типовые задачи возникают в психолого-педагогических исследованиях? 2. Какие математические методы нужны для их решения? 3. Как реализовать эти методы в SPSS?
Подчеркнем, что Московский государственный психолого-педагогический университет — это бренд, и мы не можем себе позволить предложить студентам неинтересный курс. Изучите наш курс, и вы не только приобретете новые полезные знания, но и получите удовольствие. Желаем успеха!
8 Глава 1. Введение в математическую статистику
1.1. Измерения и измерительные шкалы в психолого-педагогических исследованиях
В эмпирическом исследовании в психологии и педагогике мы получаем числовые данные — результаты измерительных процедур разного рода. Давайте разберемся, что же понимается под измерением в психологических исследованиях?
В обычной жизни, когда мы говорим «измерить» длину, объем, вес, температуру или другие физические величины, то представляем себе привычную процедуру: возьмем мерку и при помощи измерительного инструмента — линейки, мерного стакана, весов, термометра и др. — посмотрим, сколько раз она укладывается в измеряемом предмете. Однако в психологии и педагогике все не так просто. Эти науки изучают такие сложные явления и процессы, что придумать для них «мерку» практически невозможно. Кроме того, если до предмета можно дотронуться, увидеть его, ощутить его вес или температуру, то как «пощупать» воображение, «увидеть» память или «ощутить» мышление другого человека?
И все же измерения в психологии и педагогике тоже широко применяются. Уточним, что понимается при этом под измерением. Измерение — это приписывание чисел некоторым свойствам испытуемых по определенным правилам. Правила могут быть самыми разными. Например, при определении уровня развития зрительной памяти детей по методике А. Н. Леонтьева ребенку предъявляется последовательность из 10 символов — математических знаков — и предлагается их запомнить. Количество правильно воспроизведенных символов — это итоговая оценка, то есть число от 0 до 10, отражающее развитие зрительной памяти ребенка. Более сложное правило используется в методике В. И. Яшиной для определения уровня развития смысловой памяти детей. Ребенку читают текст и просят его пересказать. Исследователь оценивает пересказ ребенка по шести параметрам — понимание текста, структурирование текста, лексика, грамматика, плавность речи, самостоятельность пересказа — и за каждый из них ставится от 0 или 1, или 2 балла. Итоговая оценка — сумма баллов по всем параметрам, может варьировать, таким образом, от 0 до 12 баллов.
Зачем же нужны измерения в психологии и педагогике? Действительно, если мы работаем или просто общаемся с человеком, то его особенности заметны и без всяких тестов. Мы видим, что у одного ребенка память лучше, чем у другого, а этот взрослый более общителен, чем тот. Но несмотря на это, количество психометрических методик и тестов только растет. Почему же? Дело в том, что они позволяют сравнивать измеряемое свойство у разных испытуемых не просто «на глаз», а объективно: понятно, что воображение лучше развито у человека, получившего 15 баллов по тесту Торренса, чем у того, кто получил только 5 баллов. Объективные эмпирические данные дают возможность сделать психологическое исследование обоснованным и доказательным, позволяют проследить динамику развития детей, оценить эффективность коррекционной
9программы, проанализировать и составить отчет о работе организации и многое другое. Кроме того, они помогают установить нормы развития различных психических процессов при стандартизации тестов.
Несмотря на большое разнообразие тестов, опросников, проективных методик, их можно классифицировать. В настоящее время во всем мире применяется классификация измерительных шкал, предложенная в 1950-е годы американским ученым С. Стивенсом: 1. шкалы наименований (другие названия — номинативные, номинальные); 2. шкалы порядка (или же ранговые, ординальные); 3. шкалы интервалов; 4. шкалы отношений. В каждой последующей шкале используются не только свойства чисел предыдущей шкалы, но и дополнительные свойства, поэтому шкалы более высокого порядка, то есть имеющие больший порядковый номер, позволяют выполнять больше операций над числами и предоставляют больше возможностей для математической обработки. Номинативные и порядковые шкалы называются качественными, интервальные и шкалы отношений — количественными.
Охарактеризуем теперь шкалы каждого типа более подробно, но прежде ответим на вопрос, зачем это нужно знать исследователю? Ответ прост: для того чтобы правильно подобрать методы количественного анализа данных. Оказывается, что даже для одной и той же задачи, но при разных типах данных применяются разные методы математической обработки. Заметим, что измерения по качественным шкалам тоже можно и нужно обрабатывать количественными методами.
Измерение по шкале наименований — это просто классификация. Да-да, как это ни удивительно, но как только мы использовали классификацию испытуемых по некоторому свойству, тем самым мы уже измерили это свойство. Испытуемых группируют в классы, классам приписывают названия. Названия можно заменить на числа, то есть закодировать их. Эти числа означают только одно: принадлежит ли испытуемый к конкретному классу или нет. Сравнение чисел и арифметические операции над ними бессмысленны.
Например, если мы определили пол у дошкольников, то есть разбили группу детей на мальчиков и девочек, то мы произвели номинативное измерение. Можно оставить эти названия, но можно и заменить их числами, скажем, девочкам мы сопоставим число 1, а мальчикам число 2. Это не количество девочек или мальчиков, а просто коды или метки слов «девочка» или «мальчик». Сравнивать их не имеет смысла: нельзя быть девочкой в большей или меньшей степени. Легко понять, что вместо выбранных чисел можно взять любые другие, например, 58 и 175, ведь ничего кроме равенства или различия детей в отношении пола они не означают. Другой пример — национальность. Предположим, в нашей группе есть англичане (1), русские (2) и французы (3). Всем известно, что 1+2=3, но что может означать фраза «англичанин плюс русский равняется французу»?
Клинические диагнозы, типы темперамента, преобладающие типы психологической защиты, акцентуации характера, стили руководства, типы детских игр — все это примеры номинативных измерений.
Но какую же информацию можно извлечь из номинативных измерений, если, на первый взгляд, кроме частот попадания испытуемых в каждую категорию
10и их процентных долей от всей выборки ничего больше вычислить нельзя? И можно ли вообще классификацию считать измерением? Ответ — да, можно. Дело в том, что главную роль при математической обработке эмпирических данных играют совсем не вычисление средних или процентов и не построение графиков, а проверка статистических гипотез. Существуют статистические критерии, которые предназначены для номинативных шкал, и мы с ними обязательно познакомимся в дальнейшем.
Более тонкая шкала — шкала порядка. Порядковое измерение возможно, если экспериментатор может определить различные степени проявления измеряемого свойства. Испытуемым приписывают числа либо в прямом порядке, то есть чем сильнее выражено свойство, тем больше число, либо в обратном — чем слабее выражено свойство, тем больше число. Полученные числа можно сравнивать, но нельзя выполнять с ними арифметические операции. Равные разности чисел не отражают равных разностей в количествах измеряемого свойства. Нет единицы измерения. Для порядковых шкал также применяются соответствующие критерии проверки статистических гипотез.
Поясним это на примерах. Классический пример — конкурс красоты. Предположим, что перед нами стоят четыре девушки — Аня, Маша, Даша, Катя, — и мы просим какого-либо молодого человека проранжировать их по красоте, то есть назвать самую красивую, менее красивую и так далее. Любой молодой человек с легкостью сделает это. Пусть красивее всех он посчитал Катю, и мы присвоили ей число 100, далее оказались Аня (50), Маша (49) и, наконец, Даша (1). На первый взгляд, Дашу можно пожалеть, но все совсем не так плохо — ведь шкала порядковая. Действительно, 100–50=50, но нельзя сказать, что Катя красивее Ани на 50 каких-то единиц, ведь таких единиц не существует. Действительно, индивидуальные пристрастия в отношении женской красоты настолько расходятся, что нет ни единственно красивой женщины, ни единицы измерения красоты. Возможно даже, что другой молодой человек в соответствии со своими предпочтениями именно Дашу назовет самой красивой.
Другой классический пример — школьные оценки. Нельзя сказать, на сколько больше знаний у ученика, получившего на экзамене 5, чем у ученика, получившего 3. Примеры измерений по шкале порядка из области психологии: степень согласия с утверждением; уровень развития речи; степень мотивационной готовности к школе; самооценка степени развития коммуникативных навыков; степень обобщенности сенсорных эталонов. Примеры можно было бы продолжить, так как данный тип шкал наиболее распространен в этой области.
Порядковые шкалы могут быть более грубыми (3—5 градаций типа «низкий, средний, высокий уровень»; «ниже нормы», «норма», «выше нормы» или «абсолютно согласен, скорее согласен, не знаю, скорее не согласен, абсолютно не согласен») или более дифференцированными (от 6—8 ступенек). Последние, разумеется, предпочтительнее, так как позволяют более тонко оценить свойство. Грубые шкалы близки по свойствам к номинальным, а дифференцированные — к интервальным.
Измерение по интервальной шкале позволяет определить, на сколько единиц сильнее проявляется свойство у одного испытуемого, чем у другого. Здесь есть единица измерения. Числа можно складывать, вычитать, умножать и делить на коэффициент. Ноль не фиксирован и не указывает на отсутствие
11свойства. Отношение приписанных чисел бессмысленно, то есть мы не можем сказать, во сколько раз сильнее или слабее выражено это свойство. Забегая вперед, скажем, что нам, как правило, это и не требуется.
Классическим примером интервальной шкалы является температурная шкала Цельсия. Действительно, нулевой отметке соответствует температура таяния льда, отметке в 100 градусов — температура кипения воды. Другими словами, это температура перехода воды из твердого в жидкое агрегатное состояние и из жидкого в газообразное. Этот температурный промежуток разделен на 100 интервалов, и один такой интервал и есть один градус. Он является единицей измерения. Если вчера было 5 градусов тепла, а сегодня — 10 градусов, то мы говорим, что сегодня на 5 градусов теплее, чем вчера. Однако мы не можем сказать, что сегодня вдвое теплее, чем вчера, так как ноль в шкале Цельсия — условная точка отсчета, и она не означает отсутствия температуры вообще. Другой классический пример — летосчисление. В григорианском календаре начало отсчета — рождество Христово, в других календарях оно может быть другим. Новый год может также отмечаться не только в ночь с 31 декабря на 1 января, но и весной или осенью. Единственное, что объединяет все календари — длительность года, который продолжается 365 дней. Именно за этот период Земля совершает один оборот вокруг Солнца, и это — объективно существующая единица измерения.
По вопросу о наличии интервальных шкал в психологии мнения специалистов расходятся. Строго говоря, в психологии практически нет интервальных шкал. Действительно, единица измерения должна быть той же природы, что и измеряемое свойство, но что такое единица внимания, тревожности или креативности? Вместе с тем, с некоторой натяжкой, показатели, измеренные по хорошо дифференцированным шкалам, представляющим собой стандартизованные тесты с широким диапазоном баллов, таким как тесты интеллекта Стенфорда — Бине или Векслера, а также тест креативности Торренса, тест тревожности Спилбергера, тест депрессии Бека, тест агрессивности Басса — Дарки, принято обрабатывать как интервальные.
Наконец, в шкалах отношений по сравнению со шкалами интервалов добавляется абсолютный ноль, который означает отсутствие измеряемого свойства. В них с полученными числами можно выполнять все арифметические операции, а отношения чисел отражают количественные отношения измеряемого свойства. Классический пример такой шкалы — температура по Кельвину. Как известно, температура вещества определяется скоростью движения молекул: чем быстрее они движутся, тем температура выше. Нулевой отметкой в шкале Кельвина считается такая, при которой движение молекул прекращается — это абсолютный ноль. В психологии и педагогике такие шкалы встречаются, если измеряются физические величины — рост, вес, время решения задачи, скорость реакции на стимул, количество допущенных ошибок и другие. Шкалы отношений встречаются также в психофизике при измерении абсолютных порогов чувствительности. Добавим, что при анализе количественных измерений, то есть шкал интервалов и шкал отношений, используются одни и те же методы.
При обработке эмпирических данных в SPSS мы сначала должны указать тип измерительной шкалы. Программа SPSS предлагает на выбор три варианта: номинальные, порядковые и количественные шкалы. Если говорить совсем
12просто, номинальные измерения — это типы, порядковые — это уровни или степени, а количественные — это баллы или масштаб, то есть методики с широким диапазоном тестовых баллов. Пока шкалы не обозначены, SPSS не будет работать, зато потом он подстрахует нас: если мы попытаемся выполнить операцию, запрещенную для данного типа измерений, программа сообщит нам об этом и не будет ее выполнять.
1.2. Генеральная совокупность и выборка, графическое представление данных
В исследованиях в психологии и педагогике используется выборочный метод. Пусть мы изучаем психологические особенности некоторой категории людей. На практике обследовать всех людей этой категории невозможно по организационным, финансовым и другим причинам. Действительно, мы не можем протестировать всех детей, обучающихся по системе Монтессори, даже в нашей стране, так как детских садов слишком много. Тогда из исследуемой категории случайным образом отбирают группу испытуемых и работают с ними. Эта совокупность случайно отобранных людей называется выборкой, а категория людей, из которых производится выборка, называется генеральной совокупностью.
Уточним понятие генеральной совокупности. Иногда считается, что это просто большая группа людей, а выборка — ее подгруппа. Это не совсем так. По существу, генеральная совокупность — это множество всех мысленно возможных людей интересующего нас типа, например, детей 5-го года жизни, студентов с ограниченными возможностями здоровья (ОВЗ) или замужних женщин, психологические особенности которых мы изучаем. Давайте задумаемся, кто такие дети 5-го года жизни? Ведь время идет, дети растут и постепенно переходят в следующую возрастную категорию детей 6-го года жизни. А дети 4-го года жизни, подрастая, становятся детьми 5-го года жизни, и этот процесс бесконечен. Получается, что генеральная совокупность — это текущая река, в которой состав воды плавно, но постоянно меняется и обновляется. Точно так же, студенты с особенностями развития заканчивают обучение и покидают университет, а на их место приходят новые студенты. Замужние женщины — это вообще очень динамично меняющаяся по составу категория. Таким образом, генеральная совокупность — это скорее математическая абстракция.
Основными понятиями математической статистики являются понятия переменной, признака или случайной величины. Все эти термины используются как синонимы и означают психологические и педагогические характеристики, например, уровень тревожности, продуктивность вербальной памяти, мотивационная готовность к школе, уровень знаний по предмету и т. д. Мы говорим «переменная», потому что разные испытуемые могут набрать разное количество баллов по тесту. Даже один и тот же испытуемый в два разных момента времени может показать разные результаты. Термин «случайная величина» пришел из теории вероятностей, которая служит основой для математической статистики. Что же он означает? Действительно, когда исследователь
13тестирует испытуемого, он не может достоверно предсказать его результат, а, в лучшем случае, лишь с некоторой долей вероятности. С этой точки зрения тестирование — это процедура, похожая на бросание игрального кубика: мы не знаем заранее, сколько очков у нас выпадет. Наконец, понятие «признак», пожалуй, самое нейтральное и не нуждается в комментариях.
Несколько слов о понятии «репрезентативность выборки». Чтобы по выборке можно было уверенно судить о генеральной совокупности, она должна быть репрезентативной, т. е. достаточно хорошо, без искажений представлять генеральную совокупность. В небольших исследованиях, например, в магистерских диссертациях, репрезентативность выборки обеспечивается случайностью отбора. «Случайность отбора» означает отсутствие тенденциозности. Например, если мы изучаем интеллект или учебную мотивацию у старшеклассников и претендуем на общность выводов, то в выборку мы должны включить не только учащихся школ крупных городов, занимающих высшие места в рейтинге, но и обычных районных школ в небольших населенных пунктах. Если же у исследователя нет такой возможности, то нужно уточнить понятие генеральной совокупности, сужая его. Например, мы говорим, что исследуемая категория — это интеллектуально одаренные дети или, наоборот, дети с ментальными нарушениями. Если же изучается ситуация в некотором регионе на больших выборках, например, 4—6 тысяч человек, то обычно применяются специальные процедуры отбора. При этом пропорции испытуемых разных категорий примерно соответствуют процентному составу различных групп населения в этом регионе. Однако такие исследования — это командная работа.
Объем или размер выборки — это число испытуемых в ней. Объем генеральной совокупности обычно считается бесконечным, так как это «текущая река» без начала и конца. Выборки каких же объемов лучше использовать в реальных исследованиях? Самый общий ответ: чем больше испытуемых, тем более вероятно получить интересные доказательные результаты эмпирического исследования. Интересный результат — это, например, особенности развития речи детей с аутизмом по сравнению со здоровыми детьми; оценка эффективности коррекционной программы для младших школьников или тренинга развития партнерского общения; связь различных психических процессов или характеристик личности; влияние метода обучения на его результат и т. д. В следующих главах мы объясним, что статистические критерии лучше «видят» различия на больших выборках.
Ориентироваться на малые выборки не следует еще и потому, что серьезное научное исследование требует большой, профессионально собранной базы данных. Согласно известной русской сказке, нельзя «сварить щи из топора». Ни один солидный научный журнал не возьмет статью для публикации, если результаты получены на малых выборках, и это совершенно справедливо.
В зарубежных публикациях выборки менее 500 испытуемых почти не встречаются. Мы рекомендуем при написании магистерских диссертаций и других выпускных квалификационных работ следовать «правилу ста»: общий объем выборок в эмпирическом исследовании должен быть не менее 100 испытуемых, а еще лучше — порядка 150—200 человек. В серьезных исследованиях, проводимых
14целыми командами, объемы выборок доходят до нескольких тысяч. Именно к таким объемам и надо стремиться.
Гистограмма распределения
Пусть есть выборка, и мы хотели бы представить эту информацию графически. Если измерения количественные, чаще всего используется гистограмма.
При больших выборках удобнее обобщенное представление данных в виде распределения сгруппированных частот. Графическое изображение распределения частот попадания элементов выборки в соответствующие интервалы группировки называется частотной гистограммой выборки (далее — просто гистограммой). Иными словами, гистограмма — это совокупность столбцов, каждый из которых опирается на один разрядный интервал, а их высоты отражают частоты попадания тестовых баллов в каждый из разрядных интервалов. Покажем на примере алгоритм построения гистограммы.
Пример
Рассмотрим показатели интеллекта по тесту Стенфорда — Бине у группы из 34 испытуемых (n=34). Построить гистограмму распределения тестовых баллов.
111 | 108 | 119 | 130 | 121 | 110 | 115 |
117 | 115 | 93 | 87 | 108 | 120 | 114 |
123 | 113 | 127 | 106 | 99 | 128 | 113 |
133 | 80 | 100 | 106 | 102 | 113 | 105 |
140 | 125 | 100 | 98 | 93 | 119 | |
Идея построения гистограммы
Изобразим числовую прямую и отметим на ней тестовые баллы из нашей выборки. В любой выборке есть максимальный и минимальный баллы — мы обозначим их Xmax и Xmin. Все остальные баллы находятся между ними. Длина отрезка от минимального до максимального балла называется размахом выборки. Этот отрезок мы хотим разбить на несколько более коротких отрезков одинаковой длины и посчитать, сколько тестовых баллов попало в каждый короткий отрезок. Отрезки называются интервалами группировки, а количество попавших в них показателей — частотами. Таким образом, вся выборка делится на группы показателей в каждом интервале и получается распределение сгруппированных частот. Если его изобразить графически, получится гистограмма распределения.
Алгоритм построения гистограммы
Для построения гистограммы нужно сделать 4 шага.
1) Определить размах выборки: R=Xmax–Xmin
2) Выбрать длину интервала группировки.
3) Построить распределение сгруппированных частот.
4) Построить гистограмму распределения.
15В нашей выборке максимальный балл Xmax=140, минимальный балл Xmin=80, размах выборки R=Xmax–Xmin=140-–80=60 баллам.
Разделим наш отрезок от минимального до максимального балла, например, на 10 интервалов группировки, тогда длина одного интервала будет равна 6 баллам. Далее заполним такую таблицу:
Таблица 1.1. Распределение сгруппированных частот
Номер интервала | Границы интервала | Подсчет | Частота |
1 | [80, 86] | | | 1 |
2 | (86, 92] | | | 1 |
3 | (92, 98] | | | | | 3 |
4 | (98, 104] | | | | | | 4 |
5 | (104, 110] | | | | | | | | 6 |
6 | (110, 116] | | | | | | | | | 7 |
7 | (116, 122] | | | | | | | 5 |
8 | (122, 128] | | | | | | 4 |
9 | (128, 134] | | | | 2 |
10 | (134, 140] | | | 1 |
В первом столбце таблицы находятся порядковые номера интервалов группировки с 1-го по 10-й. Второй столбец — Границы интервалов — содержит координаты левого и правого конца интервалов. В третьем столбце — Подсчет — каждая палочка означает тестовый балл, попавший в соответствующий интервал группировки. Наконец, в последнем столбце — Частота — мы видим количество тестовых баллов, попавших в каждый интервал группировки. Очевидно, что если все частоты сложить, то должно получиться 34 балла, то есть объем выборки. Это соответствие — интервал группировки и частота — и называется распределением сгруппированных частот.
Теперь мы можем это распределение частот изобразить графически, тогда получится гистограмма. Гистограмма строится в системе координат: ось абсцисс — ось X — это ось баллов, а ось ординат — ось Y — это ось частот.
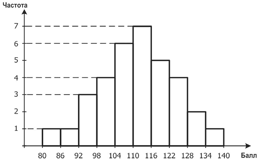
Рис. 1.1. Гистограмма распределения показателей интеллекта
На рисунке 1.1 на оси баллов отмечены концы интервалов группировки — 80, 86, 92 и так далее, — а на оси ординат — частоты попадания в них тестовых баллов.
Высота каждого столбца равна частоте тестовых баллов в этом интервале. Например, в 1-й и 2-й интервалы попали по одному баллу, в 3-й — три балла и т. д. На этом процесс построения гистограммы закончен.
Теперь возникает ряд вопросов. Что нам это дает? Чем же гистограмма лучше, чем первоначальный набор чисел — наша выборка? Гистограмма наглядно представляет распределение тестовых баллов. Например, мы видим, что в интервал [110, 116] попадает 7 тестовых баллов: это больше всего, так как там столбик самый высокий. Меньше всего тестовых баллов оказалось в интервалах [80, 86] и [86, 92], а также [134, 140] — всего по одному баллу. Вообще, баллы примерно в середине между
16минимальным и максимальным встречаются относительно чаще остальных, так как там столбики выше, а очень высокие и очень низкие баллы в выборке — реже, так как справа и слева по краям гистограммы столбики ниже. Это достаточно ожидаемая ситуация, но так бывает не всегда.
На рис. 1.2 вы видите гистограмму, построенную в SPSS.
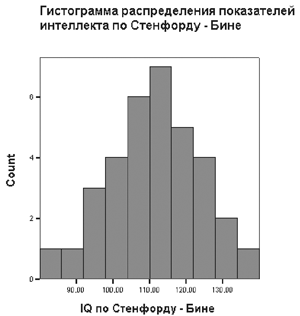
Рис. 1.2. Гистограмма распределения показателей интеллекта в SPSS
Эта гистограмма имеет особую форму: она похожа на колокол. Если бы мы захотели сгладить ее, то есть очертить плавной кривой, то эта кривая тоже была бы колоколообразной. Такие кривые играют особую роль в психологии и педагогике и имеют особое название — это нормальные кривые. Давайте дадим понятие нормальной кривой.
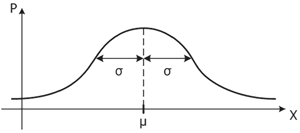
Рис. 1.3. Нормальная кривая
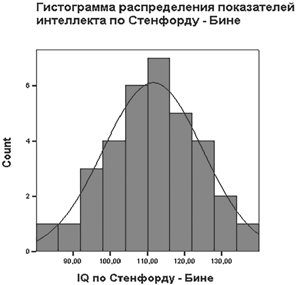
Рис. 1.4. Гистограмма и нормальная кривая
На рис. 1.3 изображена нормальная кривая. По оси X мы отмечаем тестовые баллы, по оси P — вероятность, но можно считать, что частоты. Нормальную кривую определяют 2 параметра — μ и σ. Если эта кривая отражает распределение показателей в генеральной совокупности, то μ — это генеральное среднее, а σ — это стандартное отклонение. Что же они означают графически, где их можно увидеть на рисунке? Параметр μ — это точка максимума нормальной кривой, то есть абсцисса пика кривой. Это означает, что над μ находится вершина «холма». Через μ проходит ось симметрии нормальной кривой, она обозначена пунктиром. Это значит, что если эту кривую нарисовать на листе бумаги и согнуть лист по пунктирной линии, то обе половинки кривой совпадут. Параметр σ — это расстояние от точки перегиба кривой до оси симметрии. Что же такое точка перегиба? Можно заметить, что вблизи от точки μ нормальная кривая выпукла вверх, а далеко от μ справа и слева — выпукла вниз. Следовательно, у кривой
17есть точка, где направление выпуклости меняется. Таких точек перегиба две — они симметричны относительно оси, проходящей через μ.
Что же означает, что эти два параметра определяют нормальную кривую? Чтобы это понять, давайте зафиксируем один параметр и изменим другой. Сначала зафиксируем σ, а параметр μ увеличим, как тогда изменится кривая? Очевидно, она сместится вправо вдоль оси Х, не меняя пропорций. Если μ уменьшить, то кривая сместится влево. Если же теперь μ зафиксировать, а σ увеличить, то кривая расширится и станет более плоской, а если уменьшить, то кривая сузится и станет более остроконечной. Таким образом, нормальная кривая — это не одна кривая, а целое семейство кривых, зависящих от 2-х параметров — μ и σ. Такое семейство кривых называется двупараметрическим.
Нормальные параметры вы можете видеть на рис. 1.3, гистограмму и соответствующую нормальную кривую — на рис. 1.4.
Теперь возникает вопрос: а если мы хотим построить нормальную кривую, сглаживающую нашу конкретную гистограмму, какую кривую выберет программа SPSS? Ответ прост: SPSS вычислит выборочные среднее и стандартное отклонение и построит кривую с такими параметрами μ и σ. И тогда встанет вопрос: а насколько хорошо соответствуют друг другу это нормальная кривая и гистограмма? Но ответ на этот вопрос предполагает проверку статистической гипотезы, и мы к нему вернемся позже.
Построение гистограммы в SPSS
Дана выборка показателей IQ (N=100) по тесту интеллекта Стенфорд — Бине. Построить гистограмму.
106 | 107 | 107 | 95 | 143 | 103 | 140 | 125 | 120 | 123 |
125 | 93 | 99 | 145 | 130 | 120 | 121 | 116 | 127 | 117 |
92 | 125 | 135 | 124 | 100 | 120 | 110 | 140 | 138 | 117 |
130 | 130 | 141 | 118 | 134 | 118 | 87 | 119 | 124 | 117 |
124 | 98 | 92 | 146 | 125 | 108 | 138 | 133 | 111 | 105 |
136 | 100 | 93 | 112 | 128 | 109 | 125 | 111 | 128 | 113 |
143 | 100 | 111 | 87 | 90 | 94 | 109 | 145 | 109 | 118 |
93 | 86 | 113 | 130 | 121 | 132 | 134 | 115 | 116 | 121 |
117 | 131 | 123 | 113 | 121 | 140 | 94 | 125 | 115 | 95 |
117 | 140 | 99 | 113 | 144 | 140 | 103 | 100 | 110 | 94 |
При работе в SPSS особое внимание следует уделить правильному обозначению шкалы измерений, так как программа контролирует соответствие типа шкалы выбранному методу обработки. Номинативная шкала здесь обозначается как Nominal/Номинальная, грубая порядковая шкала как Ordinal/Порядковая, а любая шкала, начиная с дифференцированной порядковой, обозначается как Scale/Количественная.
Ввод и обозначение данных. Тестовые баллы нажатием клавиши «Enter» на клавиатуре вводим в один столбец — в одну переменную, например, в первую var00001.
18
Рис. 1.5. Ввод и обозначение данных в SPSS
Для обозначения переменной нажать клавишу Variable View/Переменные в левом нижнем углу экрана. В строчке, соответствующей переменной var00001, в ячейке Name/Имя ввести имя нашей переменной, например, IQ/КИ, т. е. коэффициент интеллекта. В ячейке Label/Метка можно записать то же наименование, но можно также использовать более подробное наименование из нескольких слов, например, «intellectual quotient Stanford — Binet/коэффициент интеллекта по Стенфорду — Бине». Кроме того, нужно определить шкалу измерений в клетке Measure/Шкала: Scale/Количественная. Нажатием клавиши Data View/Данные вернуться к столбцу данных.
Рис. 1.6. Процедура построения гистограммы в SPSS
Процедура построения гистограммы. В верхней строке нажать Graphs/Графика, затем Chart Builder/Мастер диаграмм.
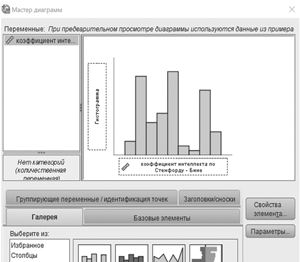
В появившемся окне, состоящем из нескольких окон, нажать кнопку Gallery/Галерея. В рамке под заголовком Choose from/Выберите из выбрать Histogram/Гистограмма. В окне правее появится несколько картинок — разных вариантов гистограмм. Выбрать самую первую картинку Simple Histogram/Простая гистограмма.
Переместить выбранную картинку в широкое окно в правом верхнем углу, над которым написано Chart preview uses example data/При предварительном просмотре диаграммы используются данные из примера. Открывается окно Element Properties/Свойства элемента. Переместить нашу переменную «intellectual quotient Stanford — Binet/коэффициент интеллекта по Стенфорду — Бине» из окошка Variables/Переменные на X-Axis/Ось Х под схематическим рисунком гистограммы, тогда на Y-Axis/Ось Y появится слово Histogram/Гистограмма.
Можно также при желании в окне Element Properties/Свойства элемента выделить X-Axis1 (Bar 1)/X-ось1 (Столбики 1) и заменить Axis Label/Метка оси на другое наименование. Можно также, но не обязательно,
19заказать Display normal curve/Вывести нормальную кривую и нажать кнопку Apply/Применить. Еще можно нажать на кнопку Titles/Footnotes — Заголовки/Сноски на гистограмме. По окончании этих процедур нажать ОК. В результате на экране появится гистограмма. Дважды щелкнув по гистограмме и используя опции Элементы и Показать метки данных, можно отредактировать гистограмму.
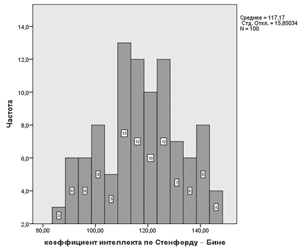
| 
|
Рис. 1.7. Процедура построения гистограммы в SPSS | Рис. 1.8. Гистограмма в SPSS с 13-ю интервалами группировки |
1.3 Статистические оценки параметров распределения
Для описания выборки помимо графиков используются информативные статистические показатели, которые описывают выборку в целом и позволяют выявить ее характерные особенности. Это удобно, так как исследователю уже не нужно просматривать сотни и тысячи отдельных баллов выборки и можно «за деревьями увидеть лес».
Среди выборочных характеристик выделяются меры центральной тенденции, меры изменчивости и меры положения. Меры центральной тенденции отражают уровень выраженности измеренного признака. К ним относятся среднее, медиана, мода. Меры изменчивости применяются для численного выражения величины вариативности признака и включают выборочные дисперсию, стандартное отклонение, асимметрию, эксцесс. Меры положения — это различные квантили, т. е точки на оси баллов, которые делят всю совокупность выборочных данных на несколько равных по численности групп с учетом частоты тестовых баллов: процентили (процентные точки) P1, P2, ..., P99 — на 100 групп, квартили Q1, Q2, Q3 — на 4 группы, децили — на 10 групп. Медиане соответствует процентиль P50, квартилям — процентили P25, P50, P75, а децилям — процентили P10, P20, ..., P90.
Выборочные характеристики — это точечные оценки параметров генеральной совокупности по выборке. Напомним, что мы изучаем генеральную совокупность, то есть некоторую категорию людей. У генеральной совокупности есть параметры, характеризующие ее как единое целое, — генеральные параметры, такие как среднее, стандартное отклонение,
20асимметрия, эксцесс. Однако мы не можем их узнать, так как генеральная совокупность нам недоступна. Действительно, если мы изучаем интеллект старшеклассников, то в генеральной совокупности старшеклассников есть среднее значение интеллекта. Как же нам его рассчитать? Точное значение определить нельзя, мы можем только оценить его приближенно по выборке. Извлечем выборку старшеклассников, найдем среднее значение интеллекта — это и будет оценка генерального среднего по этой выборке. По другой выборке получится другая оценка, по третьей — третья, но все они будут приближенно оценивать генеральное среднее. Точно так же, любая другая выборочная характеристика оценивает соответствующую генеральную. Точечной такая оценка называется, потому что это одно число — точка на числовой оси. Бывает еще оценивание генеральных параметров с помощью доверительных интервалов, но мы не рассматриваем сейчас этот метод.
Наиболее широко распространенные характеристики выборки — это среднее, дисперсия и стандартное отклонение. Реже используются медиана, мода, асимметрия и эксцесс. Среди процентилей чаще всего применяются квартили.
Рассмотрим сначала меры центральной тенденции. В психологии и педагогике они обозначаются так: среднее — M (от английского Mean), медиана — Me, Md, мода — Mo. Каждая из них по-своему означает середину, центр распределения. В математической традиции используются другие обозначения. Выборочное среднее показывает, сколько тестовых баллов в среднем получили испытуемые, и вычисляется по формуле: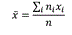 , где xi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. В действительности, это обычное среднее арифметическое, знакомое всем из курса математики начальной школы, а формула — это просто форма записи сумм однотипных слагаемых, принятая в статистике. Когда мы работаем в SPSS, мы не видим ни этой формулы, ни других: программа рассчитает все сама и сообщит результат в файле Вывода.
, где xi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. В действительности, это обычное среднее арифметическое, знакомое всем из курса математики начальной школы, а формула — это просто форма записи сумм однотипных слагаемых, принятая в статистике. Когда мы работаем в SPSS, мы не видим ни этой формулы, ни других: программа рассчитает все сама и сообщит результат в файле Вывода.
Медиана — это такое число, которое делит вариационный ряд на 2 равные части. Вариационный ряд — это последовательность тестовых баллов, расположенных в порядке возрастания, а медиана — это середина вариационного ряда. Например, у нас есть группа студентов, и мы измерили их рост. Как найти медиану этой выборки? Попросим студентов выстроиться в шеренгу по росту — это будет вариационный ряд. Измерим рост студента, который стоит в середине шеренги — это и будет медиана. Если студентов четное число, то в середине окажутся два студента. Тогда медианой будет одна вторая суммы их ростов. Поскольку слева и справа от медианы находится по 50% показателей выборки с учетом их частот, то медиана — это 50-й процентиль P50.
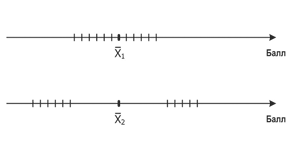
Рис. 1.9. Результаты теста двух групп испытуемых с равными средними, но разными дисперсиями
Мода — это наиболее часто встречающееся значение в выборке. Если
21в распределении только одна мода, оно называется унимодальным. Бывают распределения, в которых 2 моды — бимодальные — или несколько мод — полимодальные. На графике модам соответствуют пики гистограммы.
Меры изменчивости в психологии и педагогике принято обозначать так: дисперсия — σ2, стандартное отклонение — σ или SD (от английского Standard Deviation), асимметрия — А, эксцесс — Е. Зачем же они нужны?
Сначала зададим вопрос: достаточно ли одного среднего для описания выборки? Предположим, у нас есть 2 группы студентов, которых протестировали на знание английского языка. Распределение тестовых баллов студентов обеих групп представлено на рис. 1.9: показатели 1-й группы — сверху, показатели 2-й группы — внизу. Пусть средние в обеих группах почти совпадают, то есть в среднем обе группы показали одинаковые знания. Если же мы хотим теперь учить их английскому языку, то с какой группой нам будет работать легче? Конечно, с первой, так как там уровень знаний студентов примерно одинаков: все показатели близки к среднему. Во второй группе картина более контрастная: там есть студенты, которые знают английский очень хорошо, — их показатели справа от среднего — или, наоборот, очень плохо — показатели слева. Эта группа, фактически, разделилась на 2 подгруппы, которые надо обучать отдельно.
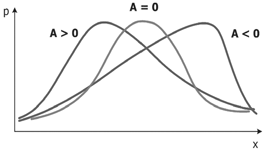
Рис. 1.10. Форма кривой распределения при разной асимметрии
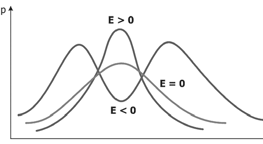
Рис. 1.11. Форма кривой распределения при разном эксцессе
Итак, нужна такая выборочная характеристика, которая позволит различать эти 2 ситуации. Она называется выборочная дисперсия и вычисляется по формуле: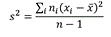 , где —
, где — 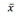 — выборочное среднее, xi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. Другими словами, это усредненная сумма квадратов отклонений тестовых баллов от среднего по выборке.
— выборочное среднее, xi — i-я по порядку варианта, ni — частота i-й варианты, n — объем выборки. Другими словами, это усредненная сумма квадратов отклонений тестовых баллов от среднего по выборке.
Предположим, мы вычислили дисперсию для некоторой выборки и получили s2=4,8. Здесь возникает 2 вопроса. Вопрос первый: это много или мало? Как это понимать? На самом деле, такой вопрос некорректен, так как нужно знать — по сравнению с чем? Дисперсия характеризует разброс показателей вокруг своего выборочного среднего: чем больше разброс, тем больше дисперсия. Если есть 2 выборки, то дисперсия больше у той, у которой баллы более рассеяны вокруг среднего.
Второй вопрос: 4,8 чего? В каких единицах выражается дисперсия. Если мы еще раз посмотрим на формулу дисперсии, то догадаемся: баллов в квадрате. На практике это не всегда удобно, поэтому в психологии и педагогике чаще используют стандартное отклонение SD или σ — квадратный корень из дисперсии. Оно
22тоже отражает рассеяние показателей вокруг среднего, но выражается в баллах. Соотношение между этими двумя характеристиками выборки видно уже из их обозначений: дисперсия — σ2, стандартное отклонение — σ.
Асимметрия характеризует «скошенность» распределения, то есть преобладание в гистограмме малых или, наоборот, больших значений признака и вычисляется по формуле: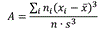 , где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу.
, где s — выборочное стандартное отклонение. Заметим, что программа SPSS использует более сложную формулу.
Знак показателя асимметрии указывает, в какую сторону отклоняется кривая распределения от симметричного вида относительно среднего значения. Если A>0, то асимметрия левосторонняя, т. е. в распределении преобладают низкие показатели. При A<0 имеем правостороннюю асимметрию с преобладанием высоких показателей. Чем больше асимметрия по модулю, тем более выражены эти тенденции. Симметричная кривая, например, нормальная, имеет А=0 (рис. 1.10).
Эксцесс — мера остроконечности или плосковершинности распределения. Он вычисляется по формуле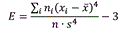 . При E>0 показатели тесно группируются на небольшом интервале, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Чем больше по модулю эксцесс, тем более выражены эти тенденции. Кривая нормального распределения имеет E=0 (рис. 1.11).
. При E>0 показатели тесно группируются на небольшом интервале, так что получается высокий «пик», а при E<0 они более далеко «расходятся» к краям, так что кривая распределения образует плоское «плато», а при больших отрицательных значениях эксцесса — даже провал, так что распределение становится бимодальным. Чем больше по модулю эксцесс, тем более выражены эти тенденции. Кривая нормального распределения имеет E=0 (рис. 1.11).
Вычисление выборочных характеристик в SPSS
Пример
Дана выборка показателей IQ (N=100) по тесту интеллекта Стенфорд — Бине. Вычислить выборочные характеристики.
106 | 107 | 107 | 95 | 143 | 103 | 140 | 125 | 120 | 123 |
125 | 93 | 99 | 145 | 130 | 120 | 121 | 116 | 127 | 117 |
92 | 125 | 135 | 124 | 100 | 120 | 110 | 140 | 138 | 117 |
130 | 130 | 141 | 118 | 134 | 118 | 87 | 119 | 124 | 117 |
124 | 98 | 92 | 146 | 125 | 108 | 138 | 133 | 111 | 105 |
136 | 100 | 93 | 112 | 128 | 109 | 125 | 111 | 128 | 113 |
143 | 100 | 111 | 87 | 90 | 94 | 109 | 145 | 109 | 118 |
93 | 86 | 113 | 130 | 121 | 132 | 134 | 115 | 116 | 121 |
117 | 131 | 123 | 113 | 121 | 140 | 94 | 125 | 115 | 95 |
117 | 140 | 99 | 113 | 144 | 140 | 103 | 100 | 110 | 94 |
23Ввод и обозначение данных. Тестовые баллы вводим в одну переменную, набирая число на клавиатуре и нажимая клавишу «Enter». Для обозначения переменной нажимаем клавишу Variable View/Переменные в левом нижнем углу экрана. Обозначим имя переменной, введя в клетку Name/Имя слово «IQ/КИ». В клетке Label/Метка опишем переменную более подробно, например, «intellectual quotient Stanford — Binet/коэффициент интеллекта по Стенфорду — Бине». Обозначим шкалу измерений Measure/Шкала: Scale/Количественная.
Вычисление выборочных характеристик. Нажмем Analyse/Анализ, затем Descriptive Statistics/Описательные статистики, Frequencies/Частоты. Выделим интересующую нас переменную и переместим ее в широкое окошко Variable(s)/Переменные. Уже заказана операция Display frequency tables/Вывести частотные таблицы (если нам это не нужно — просто отменим ее). Нажмем кнопку Statistics/Статистики, в окошке Central Tendency/Положение центра распределения отметим галочкой Mean/Среднее, Median/Медиана и Mode/Мода; в окошке Dispersion/Разброс отметим Std. Deviation/Стандартное отклонение, Variance/Дисперсия, Minimum/Минимум, Maximum/Максимум. Кроме того, закажем Quartiles/Квартили, Skewness/Асимметрия и Kurtosis/Эксцесс. Нажмем Continue/Продолжить.
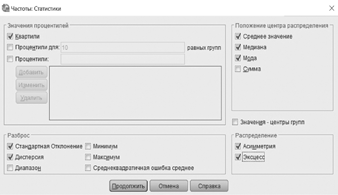
Рис. 1.12. Процедура вычисления выборочных характеристик в SPSS
Если необходимо, можно нажать кнопку Charts/Диаграммы, затем в окошке Chart Type/Тип диаграммы выбрать Histograms/Гистограммы and Show normal curve on histogram/Показать на гистограмме нормальную кривую. Нажать Continue/ and OK.
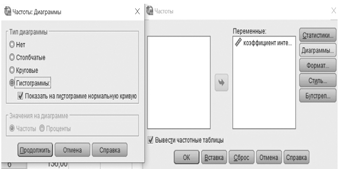
Рис. 1.13. Процедура вычисления выборочных характеристик в SPSS
В файле Вывода появится таблица с выборочными характеристиками и гистограмма (рис. 1.14 и рис. 1.15).
Статистика |
коэффициент интеллекта по Стенфорду — Бине |
N | Валидные | 100 |
Пропущенные | 0 |
Среднее | 117,1700 |
Медиана | 117,5000 |
Мода | 125,00 |
Среднекв. Отклонение | 15,85034 |
Дисперсия | 251,233 |
Асимметрия | –,085 |
Стандартная Ошибка асимметрии | ,241 |
Эксцесс | –,838 |
Стандартная ошибка эксцесса | ,478 |
Минимум | 86,00 |
Максимум | 146,00 |
Процентили | 25 | 106,2500 |
50 | 117,5000 |
75 | 129,5000 |
Рис. 1.14. Таблица с выборочными характеристиками в SPSS
24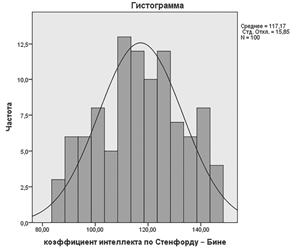
Рис. 1.15. Гистограмма с нормальной кривой в SPSS
1.4. Проверка статистических гипотез: общие положения
В психологических и педагогических исследованиях используется выборочный метод. Пусть мы хотим изучить влияние материнской поддержки интеллектуальных успехов ребенка на развитие его мышления, оценить эффективность тренинга партнерского общения или коррекционной программы для школьников с ограниченными возможностями здоровья. Возможно, наша цель — определить, какая методика лучше развивает психологическую готовность детей к школе или выявить особенности самооценки старшеклассников разного социометрического статуса. При этом неявно предполагается, что выводы будут носить общий характер и касаться не только конкретных испытуемых, но всех людей изучаемой категории. Например, такой категорией может быть определенная возрастная группа, уровень образования, социальный слой, пол и др. Очевидно, обследовать всех людей интересующей нас категории невозможно, так как их слишком много! Напомним, что «категория» на языке математической статистики называется «генеральной совокупностью». Это — математическая абстракция, и мы уже сравнивали ее с «текущей рекой» без начала и конца.
На практике в целях исследования мы извлекаем случайную выборку из генеральной совокупности. Таким образом, возникает задача изучения свойств генеральной совокупности по выборочным данным. Подчеркнем, что генеральная совокупность — это целое, а выборка — только ее часть. Как по части судить о целом, чтобы наши выводы были доказательными? В каких случаях закономерности, свойственные испытуемым выборки, могут быть обобщены на всю категорию? Для решения этой проблемы используется процедура проверки статистических гипотез.
25Под статистической гипотезой понимается высказывание о свойствах генеральной совокупности, то есть о закономерностях изучаемых процессов у определенной категории людей, проверяемое по выборке. Статистические гипотезы бывают двух видов: нулевая и альтернативная или конкурирующая. Нулевая гипотеза H0 — это выдвинутая гипотеза, подлежащая проверке. Она формулируется как предположение об отсутствии различий показателей экспериментальной и контрольной групп, отсутствии влияния фактора на отклик, отсутствии связи между признаками и т. д. Если она записывается при помощи математических символов, то в записи имеется знак равенства. Ей противопоставляется альтернативная гипотеза H1. Альтернативные гипотезы тоже бывают двух видов: ненаправленные и направленные. Ненаправленные гипотезы просто констатируют тот факт, что есть различия или влияние фактора на отклик, или связь признаков и др. Математически они записываются при помощи знака «не равно» (≠). Направленные альтернативы указывают направление различий и записываются с использованием знаков «больше» (>) или «меньше» (<).
Например, гипотеза H0: Нет различий между экспериментальной и контрольной группами по уровню креативности. Ненаправленная альтернатива H1: Различия есть. Направленная альтернатива H1: Уровень креативности в экспериментальной группе выше, чем в контрольной.
Проверкой статистической гипотезы называется процедура сопоставления эмпирических данных с выдвинутой гипотезой. В результате такой проверки мы либо принимаем H0, либо отклоняем H0 и принимаем H1. Проверка нулевой гипотезы состоит из четырех основных этапов, которые мы рассмотрим по порядку.
На первом этапе на основании эмпирических данных и задачи исследования формулируют H0 и H1. Данные могут представлять собой результаты тестирования экспериментальной и контрольной групп, и исследователя интересует, есть ли различия между ними по уровню измеренного признака. Это могут быть баллы двукратного замера некоторого параметра у одной и той же группы испытуемых на констатирующем и контрольном этапах эксперимента, и оценивается эффективность работы исследователя. Третий пример: есть баллы по двум тестам, измеряющим разные психические процессы или личностные качества, и изучается связь между ними.
Второй этап посвящен выбору статистического критерия и вычислению эмпирического значения статистики. Чтобы выбрать статистический критерий, подходящий для проверки сформулированной гипотезы H0, нужно учесть тип задачи, количество выборок и тип измерительных шкал. Как это делается, будет ясно из дальнейшего знакомства с различными критериями. По существу, статистический критерий — это правило, позволяющее однозначно установить, при каких выборках следует принять H0, а при каких — отклонить. Если же критерий выбран, тем самым выбрана статистика критерия — некоторая функция T на множестве выборок из генеральной совокупности, обладающая следующими двумя свойствами. При подстановке в нее выборочных данных функция T принимает числовые значения, и эти значения позволяют судить о расхождении экспериментальных данных с гипотезой H0. Закон распределения статистики T в предположении справедливости гипотезы H0 известен и отражен в специальных таблицах — своих для каждого критерия.
26Выражение «функция на множестве выборок» можно понимать так. Как только мы выбрали статистический критерий, например, критерий Манна — Уитни, это означает, что у нас есть формула, в которую нужно подставить данные выборки, провести вычисления и получить число Tэмп. Это и есть эмпирическое значение статистики критерия на данной выборке. Оно нам поможет сделать вывод о том, принять H0 или отклонить ее. При работе в SPSS формул мы не видим. Программа сама делает вычисления и пишет результата в файле Вывода. Как только эмпирическое значение статистики найдено, второй этап завершен.
На третьем этапе при работе в любом статистическом пакете, в том числе в SPSS, вычисляют уровень значимости. В математической традиции его принято обозначать α, а в психологии и педагогике — p (от английского probability — вероятность). Поясним, что он собой представляет.
Мы изучаем генеральную совокупность по выборке, то есть по части мы хотим сделать обоснованный вывод о целом. Очевидно, сделать это со 100%-ной уверенностью невозможно, и всегда есть риск ошибки такого вывода. Другими словами, гипотеза H0 — это предположение о свойствах генеральной совокупности, но проверяется оно по выборке, следовательно, оно может быть ошибочным. Логически возможны всего 4 варианта: 1) H0 объективно верна, и мы ее принимаем, 2) H0 верна, но мы ее отклоняем, 3) H0 неверна, но мы ее принимаем, 4) H0 неверна, и мы ее отклоняем. В первом и последнем случаях мы приходим к правильному решению, а во втором и третьем — к ошибочному. Отклонение истинной гипотезы H0 называется ошибкой 1-го рода, а принятие ложной гипотезы H0 — ошибкой 2-го рода. Вероятность совершить ошибку первого рода, то есть увидеть неслучайные различия там, где они на самом деле случайны, и называется уровнем значимости и обозначается α или p.
Уровень значимости p может принимать любые значения между 0 и 1, так как это вероятность. Среди них есть 3 значения, играющие особую роль: p=0,05, p=0,01 и p=0,001. Они называются конвенциональными уровнями значимости от слова «конвенция», то есть «договоренность» или «соглашение». Действительно, по договоренности во всем научном сообществе любое значение р принято соотносить с одним из 3-х конвенциональных уровней значимости. В любой научной статье мы увидим ссылки на них. Например, p=0,01 означает, что если гипотезу H0 проверять по каждой из 100 выборок из генеральной совокупности, то в среднем в одном случае из 100 мы совершим ошибку первого рода.
Вероятность того, что не будет допущена ошибка второго рода, называется мощностью критерия. Вероятность ошибки 2-го рода обозначается β, а мощность критерия (1–β). При математической разработке критерия он строится так, чтобы мощность критерия при фиксированном p была максимальной. Добавим, что при заданном объеме выборки уменьшить одновременно вероятности ошибок первого и второго рода, то есть p и β, невозможно: с уменьшением p вероятность β будет возрастать. Чтобы одновременно уменьшить вероятности ошибок первого и второго рода, нужно увеличить объем выборки.
Осталось пояснить, почему различают ошибки первого и второго рода.
27Оказывается, что их последствия различны. Пусть, например, при клинических испытаниях нового лекарства сформулирована гипотеза H0: «лекарство безвредно при беременности», а альтернатива H1: «лекарство вредно при беременности». Если допущена ошибка первого рода, то в инструкции к объективно безвредному при беременности лекарству будет написано «Противопоказание: беременность», и число его потенциальных покупателей сократится. Небольшие убытки понесут при этом только фармацевтическая компания и аптечные сети. Если же допущена ошибка второго рода, то беременным будет разрешено принимать опасное лекарство, что может привести к патологиям ребенка. Вот почему ошибку первого рода называют риском производителя, а ошибку второго рода — риском потребителя.
Четвертый этап — это принятие решения. Напомним, что на 2-м этапе проверки нулевой гипотезы программа SPSS вычисляет эмпирическое значение статистики, а на 3-м — соответствующий уровень значимости α. Далее действуют по правилу: если p≤0,05, то гипотезу H0 отклоняют на уровне значимости p, в противном случае H0 принимают. Это правило универсально и подходит для любого статистического критерия.
Заметим, если H0 принята, это не значит, что она доказана, но означает лишь наличие факта, говорящего в ее пользу. Одно свидетельство в пользу любой теоремы не доказывает ее справедливости. Правильнее говорить: «Эмпирические данные согласуются с нулевой гипотезой». А вот отклоняем H0 мы значительно более уверенно, ведь достаточно одного лишь контрпримера, чтобы показать, что теорема неверна. Что означает выражение: «отклонить гипотезу H0 на уровне значимости α», мы объясним на примерах при решении задач. Кроме того, в дальнейшем мы будем обозначать уровень значимости через p, а не α, как это принято в психологии и педагогике.
28 Глава 2. Одновыборочные и двухвыборочные задачи
2.1 Выявление различий между двумя независимыми выборками: критерий Манна — Уитни
Однородность двух независимых выборок
Итак, мы начинаем изучать конкретные критерии, которые используются для проверки статистических гипотез. Начнем с критерия Манна — Уитни. Это один из наиболее часто применяемых статистических критериев в психологии и педагогике. Он будет полезен для обработки эмпирических данных в ваших исследованиях с вероятностью почти 100%.
Начнем с постановки задачи. Выражаясь формально, она называется задачей однородности двух независимых выборок. Пусть у двух групп испытуемых, например, у экспериментальной и контрольной, измерен уровень креативности по тесту Торренса. Тогда у нас есть 2 ряда тестовых баллов: в левом столбце вы видите показатели экспериментальной группы, а в правом — контрольной. Баллы в экспериментальной группе обозначены x1, x2, ..., xn1, а баллы в контрольной группе — y1, y2, ..., yn2. Нас интересует, есть ли различия между двумя группами по уровню креативности? Объемы выборок n1 и n2 не обязательно равны, например, в одной группе может быть 120 человек, в другой — 250.
Теперь сформулируем ту же задачу немного более формально. Пусть имеются 2 независимые выборки x1, x2, ..., xn1 и y1, y2, ..., yn2. Есть ли различия между ними по уровню исследуемого признака? Шкала измерений должна быть не ниже порядковой и обязательно иметь широкой диапазон значений. Лучше, если шкала измерений количественная. Чем шире диапазон шкалы, тем больше информации она содержит и тем лучше критерий «видит» различия.
Что значит «две независимые выборки»? Это термин математической статистики, и он означает две разные группы испытуемых, никак не связанные между собой. Например, это экспериментальная и контрольная группы. Или это группа мужчин и группа женщин, не имеющих никакого отношения друг к другу и даже незнакомых друг с другом: например, это не могут быть семейные пары или родственники. Возможно, это 2 группы испытуемых разного возраста — от 21 до 30 лет и от 31 до 40 лет — или группа людей с средним образованием и группа с высшим образованием.
Для решения этой задачи и предназначен критерий Манна-Уитни. Более формально: критерий Манна-Уитни предназначен для сравнения показателей двух независимых выборок с целью выявления статистически значимых различий между ними по уровню исследуемого признака. Обратите внимание, что выражение «различия между выборками» — это просто краткая форма речи, которая означает различия между соответствующими генеральными совокупностями!
Сформулируем гипотезы H0 и H1. Это образец, по которому вы будете формулировать гипотезы для этого критерия в ваших исследованиях.
29H0: Нет различий между 2-мя группами по уровню исследуемого признака. Выборки взяты из одной генеральной совокупности.
H1 (НЕнаправленная): Различия есть.
H1 (направленная): Уровень признака в одной группе выше, чем в другой. В этом случае мы должны указать, в какой конкретно группе мы предполагаем более высокий уровень значений признака.
Заметим, что при работе в SPSS мы почти для всех критериев используем НЕнаправленную альтернативу за очень редким исключением. О таких исключениях позже будет сказано отдельно. На этом введение окончено. Перейдем к решению конкретных задач в SPSS.
Решение примера в SPSS
Пример 2.1
В эмпирическом исследовании кратковременной зрительной памяти были обследованы дети 7-летнего возраста с нарушениями бинокулярного зрения (N1=34 и с нормальным зрением (N2=40) с использованием следующей методики. Ребенку в течение 20 секунд показывали таблицу с 16 изображениями разнородных легко вербализуемых предметов и просили их запомнить, а затем — назвать все запомнившиеся предметы. Подсчитывалось количество правильно названных предметов. Данные представлены в таблице.
Таблица 2.1. Показатели кратковременной зрительной памяти 7-летних детей с нарушениями бинокулярного зрения и с нормальным зрением
Кратковременная зрительная память у детей 7 лет |
Дети с нарушениями
бинокулярного зрения | Дети с нормальным
зрением |
№ | Балл | № | Балл |
1 | 6 | 1 | 14 |
2 | 5 | 2 | 13 |
3 | 4 | 3 | 14 |
4 | 7 | 4 | 13 |
5 | 8 | 5 | 15 |
6 | 11 | 6 | 13 |
7 | 3 | 7 | 16 |
8 | 5 | 8 | 10 |
9 | 7 | 9 | 10 |
10 | 7 | 10 | 16 |
11 | 10 | 11 | 12 |
12 | 10 | 12 | 16 |
30
Кратковременная зрительная память у детей 7 лет |
Дети с нарушениями
бинокулярного зрения | Дети с нормальным
зрением |
№ | Балл | № | Балл |
13 | 8 | 13 | 12 |
14 | 8 | 14 | 10 |
15 | 9 | 15 | 9 |
16 | 7 | 16 | 14 |
17 | 12 | 17 | 12 |
18 | 12 | 18 | 9 |
19 | 8 | 19 | 9 |
20 | 7 | 20 | 15 |
21 | 7 | 21 | 16 |
22 | 13 | 22 | 13 |
23 | 8 | 23 | 9 |
24 | 6 | 24 | 8 |
25 | 7 | 25 | 14 |
26 | 6 | 26 | 8 |
27 | 5 | 27 | 13 |
28 | 5 | 28 | 9 |
29 | 3 | 29 | 9 |
30 | 9 | 30 | 12 |
31 | 6 | 31 | 8 |
32 | 12 | 32 | 16 |
33 | 13 | 33 | 13 |
34 | 7 | 34 | 14 |
| | | 35 | 7 |
| | | 36 | 8 |
| | | 37 | 10 |
| | | 38 | 10 |
| | | 39 | 13 |
| | | 40 | 15 |
Есть ли статистически значимые различия по уровню развития кратковременной зрительной памяти между детьми 7 лет с нарушениями бинокулярного зрения и с нормальным зрением?
Очевидно, что показатели развития кратковременной зрительной памяти в группе здоровых детей выше, но мы помним, что видимые различия могут быть результатом воздействия случайных факторов, поэтому сформулируем гипотезы.
H0: Нет различий по уровню развития кратковременной зрительной памяти между детьми 7 лет и старше с нарушениями бинокулярного зрения и с нормальным зрением. Выборки статистически однородны.
H1: Различия есть.
31Решение примера 2.1 в SPSS
Ввод и обозначение данных. Для ввода данных используется две переменных — два столбца. В первый столбец сначала вводим показатели группы детей с нарушениями бинокулярного зрения нажатием клавиши Enter на клавиатуре, затем непосредственно под ними в тот же столбец вводим показатели группы детей с нормальным зрением. Во второй столбец напротив каждого показателя вводим номер его группы — 1 или 2: он будет нашей «группирующей переменной».
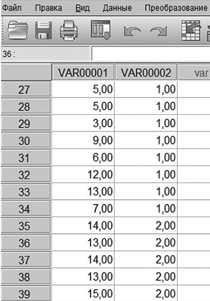
Рис. 2.1. Ввод и обозначение данных для примера 2.1 в SPSS
Для обозначения переменных в левом нижнем углу экрана нажмем кнопку Variable View/Переменные и увидим таблицу, каждая заполненная строка которой несет информацию о конкретной переменной. Обозначим первую переменную. В верхней строчке в клетке Name/Имя укажем новое имя первой переменной: «memory/память». В клетке Label/Метка можно более распространенно указать содержимое этой переменной, например, «visual memory/зрительная память». В клетке Measure/Шкала из трех предложенных типов выбираем нужный тип шкалы измерений: Scale/Количественная.
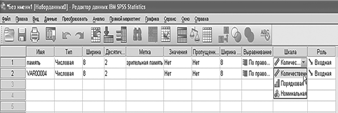
Рис. 2.2. Ввод и обозначение данных для примера 2.1 в SPSS
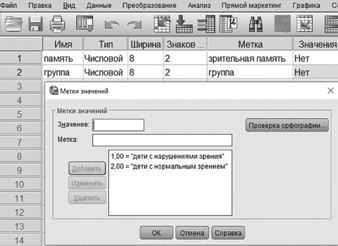
Рис. 2.3. Ввод и обозначение данных для примера 2.1 в SPSS
Вторая переменная содержит номера групп, поэтому ее Name/Имя — «group/группа», и то же название можно присвоить Label/Метке — «group/группа». Для этой переменной — она номинативная — нужно указать, какой номер соответствует какой группе. Для этого в клетке Values/Значения справа от слова None/Нет нажимаем на серый квадратик, и на экране появляется табличка. В ней в окошко Value/Значение вводим 1, в окошко Value label/Метка вводим фразу «children with visual impairment/дети с нарушениями зрения», затем нажимаем Add/Добавить, и значению 1 присваивается указанное наименование.
32Затем в окошко Value/Значение вводим число 2, в окошко Value label/Метка вводим «children with normal vision/дети с нормальным зрением». Затем нажатием кнопки ОК возвращаемся к таблице переменных.
Осталось обозначить шкалу измерений в клетке Measure/Шкала — Nominal/Номинальная. Затем возвращаемся к столбцам-переменным нажатием кнопки Data View/Данные.
Процедура проверки гипотезы. Нажатием кнопки Analyze/Анализ в верхней строке выйти в подменю и выбрать Nonparametric Tests/Непараметрические критерии, далее — Independent Samples/Для независимых выборок.
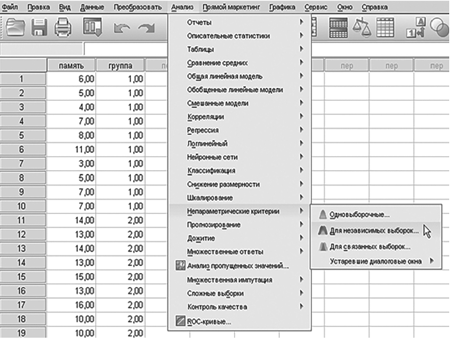
Рис. 2.4. Процедура проверки гипотезы для примера 2.1 в SPSS
Появится окно Nonparametric Tests: Two or More Independent Samples/Непараметрические критерии: две независимые выборки или более с тремя кнопками вверху: Objective/Цель, Fields/Поля и Settings/Параметры. Нажать кнопку Objective/Цель и задать Customize analysis/Задать настройки преобразований самостоятельно.
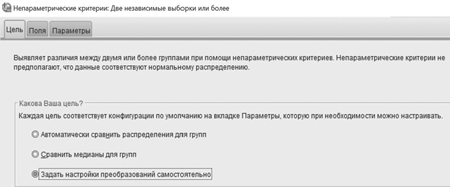
Рис. 2.5. Процедура проверки гипотезы для примера 2.1 в SPSS
Затем нажать кнопку Fields/Поля и задать Use custom field assignments/Настроить назначения полей. Все имеющиеся у нас переменные оказываются в левом широком окне Fields/Поля. Выделить нужную нам количественную переменную «visual memory/зрительная память» и нажатием на стрелку переместить ее в правое широкое окно Test Fields/Проверяемые поля. Выделить переменную «group/группа» и нажатием на стрелку переместить ее в нижнее узкое окошко Groups/Группы.
Рис. 2.6. Процедура проверки гипотезы для примера 2.1 в SPSS
Нажать на верхнюю кнопку Settings/Параметры, затем Customize tests/Настроить критерии. Отметить галочкой Mann — Whitney (2 samples)/U Манна — Уитни (для двух выборок). Нажать на кнопку Run/Запуск в самой нижней строке.
Принятие решения. На экране появляется следующая таблица.
Мы видим, что нулевая гипотеза отклоняется на уровне значимости p<0,001, таким образом, различия есть. Чтобы узнать, в какой группе уровень зрительной памяти достоверно выше, дважды щелкнем по правому желтому полю этой


























